转载:Using ES6 with gulp
Nov 2nd, 2015
- As of node 4, we’re now able to use ES2015 without the need for Babel. However modules are not currently supported so you’ll need to use `require()` still. Checkout the node docs for more info on what’s supported. If you’d like module support and to utilise Babel, read on.
- Post updated to use Babel 6.
With gulp 3.9, we are now able to use ES6 (or ES2015 as it’s now named) in our gulpfile—thanks to the awesome Babel transpiler.
Firstly make sure you have at least version 3.9 of both the CLI and local version of gulp. To check which version you have, open up terminal and type:
This should return:
CLI version 3.9.0
Local version 3.9.0
If you get any versions lower than 3.9, update gulp in your package.json file, and run the following to update both versions:
npm install gulp && npm install gulp -g
Creating an ES6 gulpfile
To leverage ES6 you will need to install Babel (make sure you have Babel 6) as a dependency to your project, along with the es2015 plugin preset:
npm install babel-core babel-preset-es2015 --save-dev
Once this has finished, we need to create a .babelrc config file to enable the es2015 preset:
And add the following to the file:
{
"presets": ["es2015"]
}
We then need to instruct gulp to use Babel. To do this, we need to rename the gulpfile.js to gulpfile.babel.js:
mv "gulpfile.js" "gulpfile.babel.js"
We can now use ES6 via Babel! An example of a typical gulp task using new ES6 features:
'use strict';
import gulp from 'gulp';
import sass from 'gulp-sass';
import autoprefixer from 'gulp-autoprefixer';
import sourcemaps from 'gulp-sourcemaps';
const dirs = {
src: 'src',
dest: 'build'
};
const sassPaths = {
src: `${dirs.src}/app.scss`,
dest: `${dirs.dest}/styles/`
};
gulp.task('styles', () => {
return gulp.src(paths.src)
.pipe(sourcemaps.init())
.pipe(sass.sync().on('error', plugins.sass.logError))
.pipe(autoprefixer())
.pipe(sourcemaps.write('.'))
.pipe(gulp.dest(paths.dest));
});
Here we have utilised ES6 import/modules, arrow functions, template strings and constants. If you’d like to check out more ES6 features, es6-features.org is a handy resource.
![]() 第k次迭代为:
第k次迭代为:![]()
![]() 为n x n对称正定矩阵,可以在每次迭代中更新。注意到这个构造函数在p=0的时候,
为n x n对称正定矩阵,可以在每次迭代中更新。注意到这个构造函数在p=0的时候,![]() 和
和![]() 和原函数是相同的。对其求导,得到
和原函数是相同的。对其求导,得到![]()
![]() 第k+1次迭代为(其中
第k+1次迭代为(其中![]() 可以用强Wolfe准则来计算):
可以用强Wolfe准则来计算):![]()
![]() (计算太复杂),Davidon提出用最近迭代的几步来计算它。
(计算太复杂),Davidon提出用最近迭代的几步来计算它。![]() ,现在构造其在k+1次迭代的二次函数:
,现在构造其在k+1次迭代的二次函数:![]()
![]() 呢?函数
呢?函数![]() 应该在
应该在![]() 处和
处和![]() 处和目标函数
处和目标函数![]() 导数一致。对其求导,并令
导数一致。对其求导,并令![]() ,即
,即![]() 处得:(
处得:(![]() 处自然相等,
处自然相等,![]() )
)![]()
![]()
![]() ,方程6为:
,方程6为:![]()
![]() ,得到另一个形式:
,得到另一个形式:![]()
![]()
![]() 的方法,令:
的方法,令:![]()
![]() 和
和![]() 为秩1或秩2的矩阵。
为秩1或秩2的矩阵。![]() 为:
为:![]()
![]()
![]()
![]() 和
和![]() 不唯一,令
不唯一,令![]() 和
和![]() 分别平行于
分别平行于![]() 和
和![]() ,即
,即![]() 和
和![]() ,带入方程11得:
,带入方程11得:![]()
![]() 和
和![]() 带入方程13得:
带入方程13得:![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() 。
。![]()
![]()
![]()
![]() 是方程中的
是方程中的![]() )(参考文档):
)(参考文档):
![]()
![]() ,方程19可得BFGS方法的迭代方程:
,方程19可得BFGS方法的迭代方程:![]()
![]() ,则BFGS方程可写成:
,则BFGS方程可写成:![]()
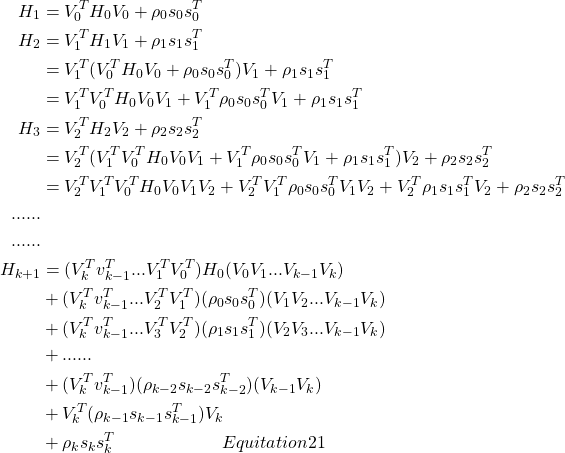
![]() 需要用到
需要用到![]() 组数据,数据量非常大,LBFGS算法就采取只去最近的m组数据来运算,即可以构造近似计算公式:
组数据,数据量非常大,LBFGS算法就采取只去最近的m组数据来运算,即可以构造近似计算公式: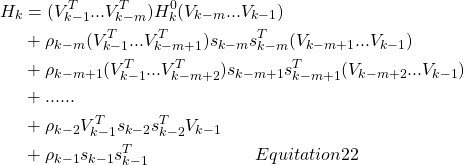
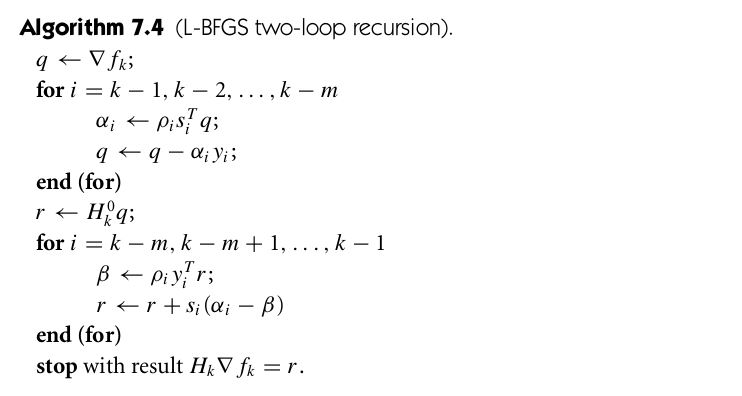
![]() :
: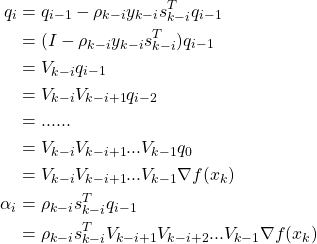
![]() ,这里的m指的是从现在到历史记录m次的后一次,因为LBFGS只记录m次历史:
,这里的m指的是从现在到历史记录m次的后一次,因为LBFGS只记录m次历史: