原创文章,转载请注明: 转载自慢慢的回味
本文链接地址: Cartesian与Frenet坐标系转换公式推导
车在道路上行驶,以车的视角来看,车就如同在一条光滑的曲线上移动,且不时带有左右偏移。为了算法简单,我们选择了Frenet坐标系,它可以把直角坐标系下的复杂轨迹转换为只有S,L两个维度的简单曲线。
Frenet坐标系简介
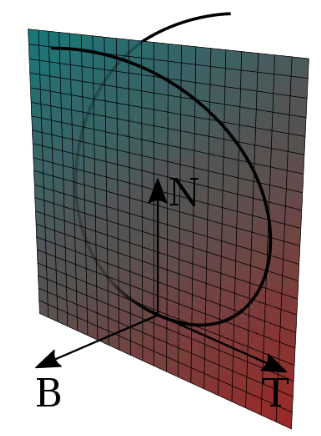
如下图所示,3维空间中一条连续可微的曲线K,P为曲线K上的一个点,方格背景平面为曲线K在点P处的运动平面。![]() 为曲线K在点P处的切向量,即质点再P处的运动方向;
为曲线K在点P处的切向量,即质点再P处的运动方向;![]() 为K在P处的法向量,垂直于质点运动方向
为K在P处的法向量,垂直于质点运动方向![]() ,
,![]() 和
和![]() 在同一运动平面;
在同一运动平面;![]() 为曲线K在P处的副法向量,且同时垂直于
为曲线K在P处的副法向量,且同时垂直于![]() 和
和![]() ,即垂直于运动平面。
,即垂直于运动平面。
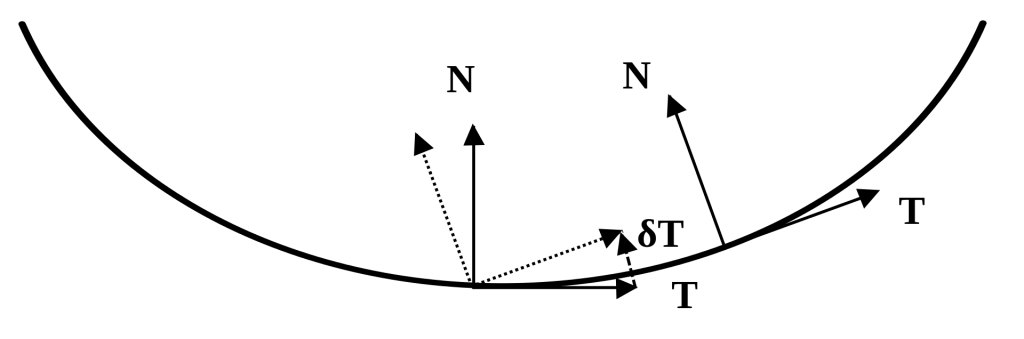
Frenet的定义公式如下:
![Rendered by QuickLaTeX.com \[ \begin{Bmatrix} \frac{d\vec{T}}{ds}= & \kappa\vec{N} \\ \frac{d\vec{N}}{ds}= & -\kappa\vec{T}+\tau\vec{B} \\ \frac{d\vec{B}}{ds}= & -\tau\vec{N} \end{Bmatrix} \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-d8c6e96d3b90832c0ffe3e7efc0091e6_l3.png)
其中,![]() 表示某一方向向量对弧长s的导数,
表示某一方向向量对弧长s的导数,![]() 为曲率为曲线相对于直线的弯曲程度,当为0时为直线,表述为曲线运动方向的变化关于弧长的导数(
为曲率为曲线相对于直线的弯曲程度,当为0时为直线,表述为曲线运动方向的变化关于弧长的导数(![]() ),
),![]() 为挠率是曲线不能形成在同一平面内运动曲线的度量值,挠率越趋于0,则曲线越趋近于在同一平面内运动。Apollo的运动在大地上,局部路面可看作一个平面,挠率可设定为0,而Frenet公式可简化为:
为挠率是曲线不能形成在同一平面内运动曲线的度量值,挠率越趋于0,则曲线越趋近于在同一平面内运动。Apollo的运动在大地上,局部路面可看作一个平面,挠率可设定为0,而Frenet公式可简化为:
(1) ![Rendered by QuickLaTeX.com \[ \begin{Bmatrix} \frac{d\vec{T}}{ds}= & \kappa\vec{N} \\ \frac{d\vec{N}}{ds}= & -\kappa\vec{T} \end{Bmatrix} \right \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-f2f0d87facdb2f33ec934e85316e6cca_l3.png)
Cartesian与Frenet坐标系转换公式推导
整个公式的推导以下图的标注为蓝图:
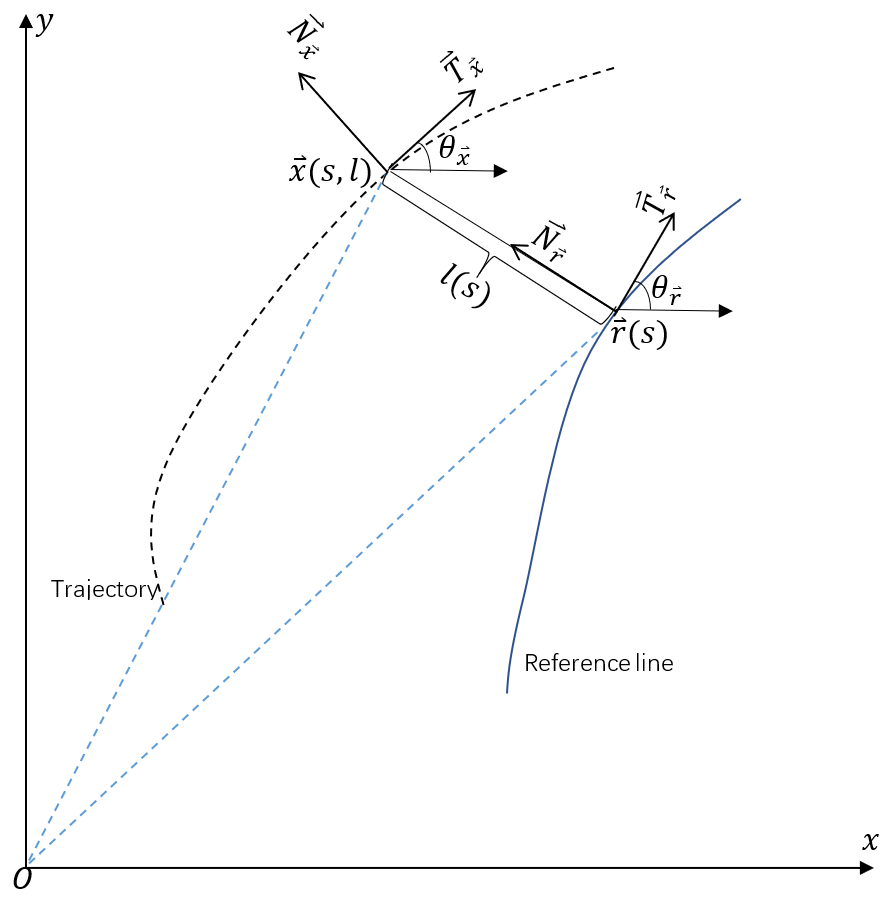
有如下变量:
Frenet坐标系:![]() ;
;
Cartesian坐标系:![]() 。
。
其中:
![]() :Frenet纵坐标,即曲线Reference Line上质点运动的位置;
:Frenet纵坐标,即曲线Reference Line上质点运动的位置;
![]() :Frenet纵坐标对时间的导数,也即沿Reference Line的速度;
:Frenet纵坐标对时间的导数,也即沿Reference Line的速度;
![]() :沿Reference Line的加速度;
:沿Reference Line的加速度;
![]() :Frenet横坐标,质点横向的偏移量;
:Frenet横坐标,质点横向的偏移量;
![]() :Frenet横向速度;
:Frenet横向速度;
![]() :Frenet横向加速度;
:Frenet横向加速度;
![]() :Frenet横向坐标对纵向坐标的导数;
:Frenet横向坐标对纵向坐标的导数;
![]() :Frenet横向坐标对纵向坐标的二阶导数;
:Frenet横向坐标对纵向坐标的二阶导数;
![]() :为对应Cartesian坐标系下的坐标,是一个向量;
:为对应Cartesian坐标系下的坐标,是一个向量;
![]() :Cartesian坐标系下的运动方向角;
:Cartesian坐标系下的运动方向角;
![]() :曲率;
:曲率;
![]() :Cartesian坐标系下的线速度;
:Cartesian坐标系下的线速度;
![]() :Cartesian坐标系下的加速度。
:Cartesian坐标系下的加速度。
如下为Apollo代码中从cartesian到frenet的转换方法:
ptr_s_condition分别存储![]() ,
,![]() 和
和![]() ;
;
ptr_d_condition分别存储![]() ,
,![]() 和
和![]() 。
。
void CartesianFrenetConverter::cartesian_to_frenet( const double rs, const double rx, const double ry, const double rtheta, const double rkappa, const double rdkappa, const double x, const double y, const double v, const double a, const double theta, const double kappa, std::array<double, 3>* const ptr_s_condition, std::array<double, 3>* const ptr_d_condition) { const double dx = x - rx; const double dy = y - ry; const double cos_theta_r = std::cos(rtheta); const double sin_theta_r = std::sin(rtheta); const double cross_rd_nd = cos_theta_r * dy - sin_theta_r * dx; ptr_d_condition->at(0) = std::copysign(std::sqrt(dx * dx + dy * dy), cross_rd_nd); const double delta_theta = theta - rtheta; const double tan_delta_theta = std::tan(delta_theta); const double cos_delta_theta = std::cos(delta_theta); const double one_minus_kappa_r_d = 1 - rkappa * ptr_d_condition->at(0); ptr_d_condition->at(1) = one_minus_kappa_r_d * tan_delta_theta; const double kappa_r_d_prime = rdkappa * ptr_d_condition->at(0) + rkappa * ptr_d_condition->at(1); ptr_d_condition->at(2) = -kappa_r_d_prime * tan_delta_theta + one_minus_kappa_r_d / cos_delta_theta / cos_delta_theta * (kappa * one_minus_kappa_r_d / cos_delta_theta - rkappa); ptr_s_condition->at(0) = rs; ptr_s_condition->at(1) = v * cos_delta_theta / one_minus_kappa_r_d; const double delta_theta_prime = one_minus_kappa_r_d / cos_delta_theta * kappa - rkappa; ptr_s_condition->at(2) = (a * cos_delta_theta - ptr_s_condition->at(1) * ptr_s_condition->at(1) * (ptr_d_condition->at(1) * delta_theta_prime - kappa_r_d_prime)) / one_minus_kappa_r_d; } |
已知![Rendered by QuickLaTeX.com \vec{x}=[x_{x}, y_{x}]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-199553cfd073e2c7e0973ce7636ca70e_l3.png) 推导
推导![Rendered by QuickLaTeX.com [s, l]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-1c1a8cc4b9c7ae1daf6b22f01a875061_l3.png)
求
通过找到曲线上离![]() 最近的参考点
最近的参考点![]() ,该参考点处的
,该参考点处的![]() 即为
即为![]() 在Frenet坐标系下的
在Frenet坐标系下的![]() 。这可以通过高清地图上路径的投影找到:
。这可以通过高清地图上路径的投影找到:
Apollo的代码如下:
bool ReferenceLine::XYToSL(const common::math::Vec2d& xy_point, SLPoint* const sl_point) const { double s = 0.0; double l = 0.0; if (!map_path_.GetProjection(xy_point, &s, &l)) { AERROR << "Cannot get nearest point from path."; return false; } sl_point->set_s(s); sl_point->set_l(l); return true; } |
求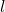
![]() 分别为参考点与待转换点在Cartesian坐标系下的向量,它们的关系为:
分别为参考点与待转换点在Cartesian坐标系下的向量,它们的关系为:![]() ,即质点
,即质点![]() 朝着
朝着![]() 的方向移动距离
的方向移动距离![]() 为
为![]() :
:
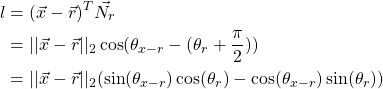
上式中,![]() 为向量
为向量![]() 的方向角度,
的方向角度,![]() 为单位向量
为单位向量![]() 的方向角度(对比上一张图可知),则上式可利用向量点乘公式
的方向角度(对比上一张图可知),则上式可利用向量点乘公式![]() 得到。
得到。![]() 为向量
为向量![]() 与向量
与向量![]() 之间的夹角。
之间的夹角。
设![]() ,则
,则![]() 。
。
在Frenet坐标系下,每个点到Reference Line上参考点的向量都与该参考点的法向量![]() 同向或反向,因为我们找的是到Reference Line的最近点,因此,
同向或反向,因为我们找的是到Reference Line的最近点,因此,![]() =1 或 -1。
=1 或 -1。![]() 为向量
为向量![]() 的角度,因此,
的角度,因此,![]() 。即可根据
。即可根据![]() 的正负来确定
的正负来确定![]() 的正负号,公式如下:
的正负号,公式如下:
(2) ![]()
已知![Rendered by QuickLaTeX.com \vec{x}=[x_{x}, y_{x}],\theta_{x},v_x](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-d5e48968f469bc567e1c4b5774e67311_l3.png) 推导
推导![Rendered by QuickLaTeX.com [s, l,\dot{s},l']](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-fef73b62410b30648f1e5b877bf93269_l3.png)
求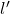
由![]() 可得:
可得:
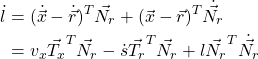
由Frenet公式(见上式式(1))有![]() ,于是有
,于是有![]() ,代入上式可得:
,代入上式可得:
![]()
由于![]() 与
与![]() 正交
正交![]() ,
,![]() ,代入上式得:
,代入上式得:
(3) ![]()
由于:
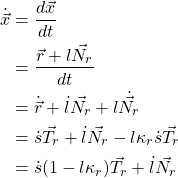
(16) ![Rendered by QuickLaTeX.com \begin{align*} v_{x} &=||\dot{\vec{x}}||_{2} \\ &=\sqrt{\dot{\vec{x}}^{T}\dot{\vec{x}}} \\ &=\sqrt{[\dot{s}(1-\kappa_{r}l)]^{2}+\dot{l}^{2}} \end{align*}](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-9661e7573a40fb049a7f126a4bdfa801_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} l'^{2} &=(\frac{dl}{ds})^{2}=(\frac{\dot{l}}{\dot{s}})^{2} \\ &=(\frac{v_{x}\sin(\theta_{x}-\theta_{r})}{\dot{s}})^{2} \\ &=\sin^{2}(\theta_{x}-\theta_{r})\frac{[\dot{s}(1-\kappa_{r}l)]^{2}+\dot{l}^{2}}{\dot{s}^{2}} \\ &=\sin^{2}(\theta_{x}-\theta_{r})[(1-\kappa_{r}l)^{2}+(\frac{\dot{l}}{\dot{s}})^{2}] \\ &=\sin^{2}(\theta_{x}-\theta_{r})[(1-\kappa_{r}l)^{2}+l'^{2}] \\ &\Rightarrow \frac{1}{\sin^{2}(\theta_{x}-\theta_{r})}l'^{2}=(1-\kappa_{r}l)^{2}+l'^{2} \\ &\Rightarrow (\frac{1}{\sin^{2}(\theta_{x}-\theta_{r})}-1)l'^{2}=(1-\kappa_{r}l)^{2} \\ &\Rightarrow \frac{\s\cos^{2}(\theta_{x}-\theta_{r})}{\sin^{2}(\theta_{x}-\theta_{r})}l'^{2}=(1-\kappa_{r}l)^{2} \\ &\Rightarrow l'=(1-\kappa_{r}l)\tan(\theta_{x}-\theta_{r}) \end{align*}](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-85c083f96b2e605bc0a3f1fe9663182b_l3.png)
因此:
(4) ![]()
求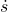
由![]() 与
与![]() 可得:
可得:
(5) ![]()
已知![Rendered by QuickLaTeX.com \vec{x}=[x_{x}, y_{x}],\theta_{x},v_x,a_x,\kappa_{x}](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-dc1e605bcf9cef83edfd96017e340b08_l3.png) 推导
推导![Rendered by QuickLaTeX.com [s, l,\dot{s},l',\ddot{s},l'']](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-92ed6d2b4e0eb8d214d7b7dd913f1687_l3.png)
求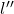
由![]() ,可得:
,可得:
(10) ![]()
假定![]() 为为车辆当前轨迹
为为车辆当前轨迹![]() 的弧长,有:
的弧长,有:
(11) ![]()
又有曲率:
(12) ![]()
(13) ![]()
故式10可得:
(14) ![]()
由式11和式13:
(15) ![]()
综上14和15可得:
(6) ![]()
求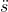
由式5得:
![]()
有三角公式的导数:
![]()
由式12和式15:
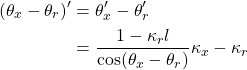
由式4得 ![]() :
:
(17) ![Rendered by QuickLaTeX.com \begin{align*} a_{x} &=\frac{dv_{x}}{dt} \\ &=\ddot{s}\frac{1-\kappa_{r}l}{\cos(\theta_{x}-\theta_{r})}+\dot{s}\frac{d}{ds}\frac{1-\kappa_{r}l}{\cos(\theta_{x}-\theta_{r})}\dot{s} \\ &=\ddot{s}\frac{1-\kappa_{r}l}{\cos(\theta_{x}-\theta_{r})}+\frac{\dot{s}^{2}}{\cos(\theta_{x}-\theta_{r})}\left[(1-\kappa_{r}l)\tan(\theta_{x}-\theta_{r})(\theta_{x}-\theta_{r})'-(\kappa_{r}'l+\kappa_{r}l')\right] \\ &=\ddot{s}\frac{1-\kappa_{r}l}{\cos(\theta_{x}-\theta_{r})}+\frac{\dot{s}^{2}}{\cos(\theta_{x}-\theta_{r})}\left[l'(\theta_{x}-\theta_{r})'-(\kappa_{r}'l+\kappa_{r}l')\right] \\ &=\ddot{s}\frac{1-\kappa_{r}l}{\cos(\theta_{x}-\theta_{r})}+\frac{\dot{s}^{2}}{\cos(\theta_{x}-\theta_{r})}\left[l'(\kappa_{x}\frac{1-\kappa_{r}l}{\cos(\theta_{x}-\theta_{r})}-\kappa_{r})-(\kappa_{r}'l+\kappa_{r}l')\right] \end{align*}](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-e7b34acc8b98f4247400f85ca68635e4_l3.png)
(7) ![Rendered by QuickLaTeX.com \[ \ddot{s}=\frac{a_{x}\cos(\theta_{x}-\theta_{r})-\dot{s}^{2}\left[l'(\kappa_{x}\frac{1-\kappa_{r}l}{\cos(\theta_{x}-\theta_{r})}-\kappa_{r})-(\kappa_{r}'l+\kappa_{r}l')\right]}{1-\kappa_{r}l} \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-edd3ecc67a2f1aaf153bb053b06fad4b_l3.png)
由式5,7,2,4,6得到Cartesian转Frenet坐标系公式:
(8) ![Rendered by QuickLaTeX.com \[ \begin{Bmatrix} s=& s_{r} \\ \dot{s}=& \frac{v_{x}\cos(\theta_{x}-\theta_{r})}{1-k_{r}l} \\ \ddot{s}=& \frac{a_{x}\cos(\theta_{x}-\theta_{r})-\dot{s}^{2}\left[l'(k_{x}\frac{1-k_{r}l}{\cos(\theta_{x}-\theta_{r})}-k_{r})-(k_{r}'l+k_{r}l')\right]}{1-k_{r}l} \\ l=& sign\left((y_{x}-y_{r})\cos(\theta_{r})-(x_{x}-x_{r})\sin(\theta_{r})\right)\sqrt{(x_{x}-x_{r})^2+(y_{x}-y_{r})^2} \\ l'=& (1-k_{r}l)\tan(\theta_{x}-\theta_{r}) \\ l''= &-(k_{r}'l+k_{r}l')\tan(\theta_{x}-\theta_{r})+\frac{(1-k_{r}l)}{\cos^2(\theta_{x}-\theta_{r})}(\frac{1-k_{r}l}{\cos(\theta_{x}-\theta_{r})}k_{x}-k_{r}) \end{Bmatrix} \right. \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-15a2ab1f2f17402a20d5ccd562d30d66_l3.png)
由式2,4,16,17,6得到Frenet转Cartesian坐标系公式:
(9) ![Rendered by QuickLaTeX.com \[ \begin{Bmatrix} x_{x}= & x_{r}-l\sin(\theta_{r}) \\ y_{x}= & y_{r}+l\cos(\theta_{r}) \\ \theta_{x}= & \arctan(\frac{l'}{1-\kappa_{r}l})+\theta_{r} \in [-\pi, \pi] \\ v_{x}= &\sqrt{[\dot{s}(1-\kappa_{r}l)]^{2}+(\dot{s}l')^{2}} \\ a_{x}= &\ddot{s}\frac{1-\kappa_{r}l}{\cos(\theta_{x}-\theta_{r})}+\frac{\dot{s}^{2}}{\cos(\theta_{x}-\theta_{r})}\left[l'(\kappa_{x}\frac{1-\kappa_{r}l}{\cos(\theta_{x}-\theta_{r})}-\kappa_{r})-(\kappa_{r}'l+\kappa_{r}l')\right] \\ \kappa_{x}= & ((l''+(\kappa_{r}'l+\kappa_{r}l')\tan(\theta_{x}-\theta_{r}))\frac{\cos^{2}(\theta_{x}-\theta_{r})}{1-\kappa_{r}l}+\kappa_{r})\frac{\cos(\theta_{x}-\theta_{r})}{1-\kappa_{r}l} \end{Bmatrix} \right. \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-de72464ef72cca90deb0a45e7241c3bb_l3.png)
参考链接:
https://blog.csdn.net/u013468614/article/details/108748016
https://blog.csdn.net/davidhopper/article/details/79162385本作品采用知识共享署名 4.0 国际许可协议进行许可。