每日归档： 2022年2月17日

Cartesian与Frenet坐标系转换公式推导

原创文章，转载请注明： 转载自慢慢的回味

本文链接地址: Cartesian与Frenet坐标系转换公式推导

车在道路上行驶，以车的视角来看，车就如同在一条光滑的曲线上移动，且不时带有左右偏移。为了算法简单，我们选择了Frenet坐标系，它可以把直角坐标系下的复杂轨迹转换为只有S，L两个维度的简单曲线。

目录:
  1. Frenet坐标系简介
  2. Cartesian与Frenet坐标系转换公式推导
    1. 已知\(\vec{x}=[x_{x}, y_{x}]\)推导\([s, l]\)
      1. 求\(s\)
      2. 求\(l\)
    2. 已知\(\vec{x}=[x_{x}, y_{x}],\theta_{x},v_x\)推导\([s, l,\dot{s},l']\)
      1. 求\(l'\)
      2. 求\(\dot{s} \)
    3. 已知\(\vec{x}=[x_{x}, y_{x}],\theta_{x},v_x,a_x,\kappa_{x} \)推导\([s, l,\dot{s},l',\ddot{s},l'']\)
      1. 求\(\l''\)
      2. 求\(\ddot{s}\)

Frenet坐标系简介

如下图所示，3维空间中一条连续可微的曲线K，P为曲线K上的一个点，方格背景平面为曲线K在点P处的运动平面。\vec{T}为曲线K在点P处的切向量，即质点再P处的运动方向；\vec{N}为K在P处的法向量，垂直于质点运动方向\vec{T}，\vec{N}和\vec{T}在同一运动平面；\vec{B}为曲线K在P处的副法向量，且同时垂直于\vec{T}和\vec{N}，即垂直于运动平面。


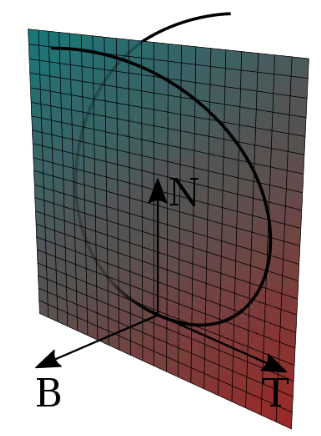
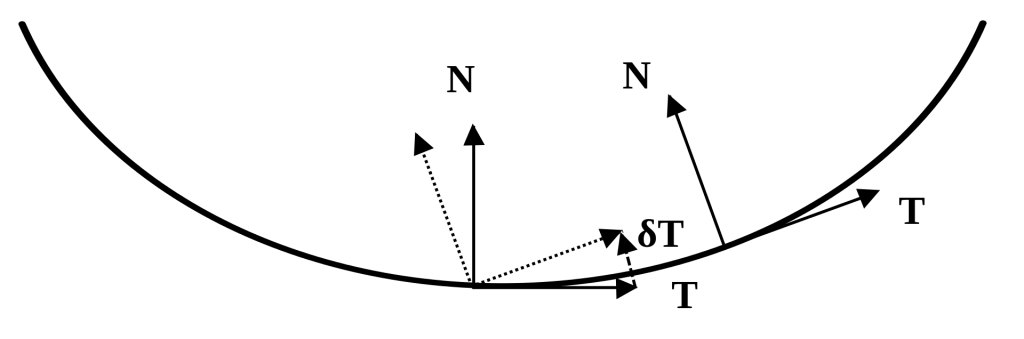
Frenet的定义公式如下：

    \[ \begin{Bmatrix} \frac{d\vec{T}}{ds}= & \kappa\vec{N} \\ \frac{d\vec{N}}{ds}= & -\kappa\vec{T}+\tau\vec{B} \\ \frac{d\vec{B}}{ds}= & -\tau\vec{N} \end{Bmatrix} \]

其中，\frac{d}{ds}表示某一方向向量对弧长s的导数，\kappa为曲率为曲线相对于直线的弯曲程度，当为0时为直线，表述为曲线运动方向的变化关于弧长的导数（\kappa = \left\| \frac {d\mathbf {T} }{ds}}\right\|），\tau为挠率是曲线不能形成在同一平面内运动曲线的度量值，挠率越趋于0，则曲线越趋近于在同一平面内运动。Apollo的运动在大地上，局部路面可看作一个平面，挠率可设定为0，而Frenet公式可简化为：

(1)   \[ \begin{Bmatrix} \frac{d\vec{T}}{ds}= & \kappa\vec{N} \\ \frac{d\vec{N}}{ds}= & -\kappa\vec{T} \end{Bmatrix} \right \]

继续阅读“Cartesian与Frenet坐标系转换公式推导”本作品采用知识共享署名 4.0 国际许可协议进行许可。