原创文章,转载请注明: 转载自慢慢的回味
Apollo里面最重要的模块就是感知和规划模块,规划模块最重要的是路径规划和速度规划任务,对应ROS机器人里面的局部规划。Apollo的规划模块首先根据当前的情况进行多场景(scenario)调度,每个场景又包含一个或者多个阶段(stage),每个阶段又由多个具有独立功能的小模块任务(task)完成。这篇文章就主要解读一下路径规划piecewise jerk path optimizer这个任务。任务最终会生成轨迹(trajectory):每个点的位姿和速度信息,进而输出给控制模块去控制车辆。
任务代码调用入口
比如通过测试用例可得到如下的堆栈:
apollo::planning::PiecewiseJerkPathOptimizer::Process(apollo::planning::PiecewiseJerkPathOptimizer * const this, const apollo::planning::SpeedData & speed_data, const apollo::planning::ReferenceLine & reference_line, const apollo::common::TrajectoryPoint & init_point, const bool path_reusable, apollo::planning::PathData * const final_path_data) (piecewise_jerk_path_optimizer.cc:61) apollo::planning::PathOptimizer::Execute(apollo::planning::PathOptimizer * const this, apollo::planning::Frame * frame, apollo::planning::ReferenceLineInfo * const reference_line_info) (path_optimizer.cc:45) apollo::planning::scenario::lane_follow::LaneFollowStage::PlanOnReferenceLine(apollo::planning::scenario::lane_follow::LaneFollowStage * const this, const apollo::common::TrajectoryPoint & planning_start_point, apollo::planning::Frame * frame, apollo::planning::ReferenceLineInfo * reference_line_info) (lane_follow_stage.cc:167) apollo::planning::scenario::lane_follow::LaneFollowStage::Process(apollo::planning::scenario::lane_follow::LaneFollowStage * const this, const apollo::common::TrajectoryPoint & planning_start_point, apollo::planning::Frame * frame) (lane_follow_stage.cc:116) apollo::planning::scenario::Scenario::Process(apollo::planning::scenario::Scenario * const this, const apollo::common::TrajectoryPoint & planning_init_point, apollo::planning::Frame * frame) (scenario.cc:76) apollo::planning::PublicRoadPlanner::Plan(apollo::planning::PublicRoadPlanner * const this, const apollo::common::TrajectoryPoint & planning_start_point, apollo::planning::Frame * frame, apollo::planning::ADCTrajectory * ptr_computed_trajectory) (public_road_planner.cc:38) apollo::planning::OnLanePlanning::Plan(apollo::planning::OnLanePlanning * const this, const double current_time_stamp, const std::vector<apollo::common::TrajectoryPoint, std::allocator<apollo::common::TrajectoryPoint> > & stitching_trajectory, apollo::planning::ADCTrajectory * const ptr_trajectory_pb) (on_lane_planning.cc:572) apollo::planning::OnLanePlanning::RunOnce(apollo::planning::OnLanePlanning * const this, const apollo::planning::LocalView & local_view, apollo::planning::ADCTrajectory * const ptr_trajectory_pb) (on_lane_planning.cc:417) apollo::planning::PlanningTestBase::RunPlanning(apollo::planning::PlanningTestBase * const this, const std::__cxx11::string & test_case_name, int case_num, bool no_trajectory_point) (planning_test_base.cc:229) apollo::planning::SunnyvaleBigLoopTest_keep_clear_02_Test::TestBody(apollo::planning::SunnyvaleBigLoopTest_keep_clear_02_Test * const this) (sunnyvale_big_loop_test.cc:191) |
二次规划定义
二次规划问题的定义如下:
![]()
![]()
Apollo使用osqp进行二次规划问题的求解。第一行为代价函数,第二行为约束条件。二次优化的目标就是在满足约束条件的基础上,找到优化变量使得代价函数的值最小。二次规划只在代价函数为凸函数的时候能够收敛到最优解,因此这需要P矩阵为半正定矩阵,这是非常重要的一个条件。这反映在Apollo中的规划算法则为需要进行求解的空间为凸空间,这样二次规划才能收敛到一条最优路径。
Apollo 中二次规划问题的构造
首先列出代价函数:
![Rendered by QuickLaTeX.com \[ J=w_x\sum^{n-1}_{i=0}(x_i-r_i)^2+w_{x'}\sum^{n-1}_{i=0}(x'_i)^2+w_{x''}\sum^{n-1}_{i=0}(x''_i)^2+w_{x'''}\sum^{n-2}_{i=0}(x'''_i)^2 \qquad\qquad\qquad Equitation 3 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-e2638ae35c0cc3d08c9ba5d9752435ce_l3.png)
其中 ![]() 表示侧向偏移量,
表示侧向偏移量,![]() 为参考偏移量。
为参考偏移量。 ![]() 分别表示侧向偏移量对路径
分别表示侧向偏移量对路径![]() 的一阶导(侧向速度)、二阶导(侧向加速度)和三阶导(侧向加加速度,由车辆的yaw角动量控制)。
的一阶导(侧向速度)、二阶导(侧向加速度)和三阶导(侧向加加速度,由车辆的yaw角动量控制)。
由 ![]() ,得到
,得到 ![]() ,将其带入J中,可得
,将其带入J中,可得
![Rendered by QuickLaTeX.com \[ J=w_x\sum^{n-1}_{i=0}[(x_i)^2+(r_i)^2-2x_ir_i]+w_{x'}\sum^{n-1}_{i=0}(x'_i)^2+w_{x''}\sum^{n-1}_{i=0}(x''_i)^2+\frac{w_{x'''}}{\Delta s^2}\sum^{n-2}_{i=0}[(x''_{i+1})^2+(x''_i)^2-2x''_{i+1}x''_i] \qquad\qquad\qquad Equitation 4 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-acfa0d502def01b783c1b48eac2036c7_l3.png)
公式4整理可得(去掉常数项):
![Rendered by QuickLaTeX.com \[ J=w_x\sum^{n-1}_{i=0}[(x_i)^2-2x_ir_i]+w_{x'}\sum^{n-1}_{i=0}(x'_i)^2+(w_{x''}+\frac{2w_{x'''}}{\Delta s^2})\sum^{n-1}_{i=0}(x''_i)^2-\frac{w_{x'''}}{\Delta s^2}(x''_0+x''_{n-1})-\frac{2w_{x'''}}{\Delta s^2}\sum^{n-2}_{i=0}(x''_{i+1}x''_i) \qquad\qquad\qquad Equitation 5 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-d26592350dc879eb19bfcc5cd57af51e_l3.png)
令:
![Rendered by QuickLaTeX.com \[ x=\begin{bmatrix} x_0 \\[4pt] x_1\\[4pt]\vdots \\[4pt]x_{n-1}\\[4pt]x'_0\\[4pt]x'_1\\[4pt]\vdots\\[4pt]x'_{n-1}\\[4pt]x''_0\\[4pt]x''_1\\[4pt]\vdots\\[4pt]x''_{n-1} \end{bmatrix}\in R^{3n \times 1} \qquad\qquad\qquad Equitation 6 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-5f57fff4bdf26ce3b6e3925535b0c927_l3.png)
则:
![Rendered by QuickLaTeX.com \[ P_x=\begin{bmatrix} w_x &0& \ldots&0\\0&w_x&\ldots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\ldots&w_x \end{bmatrix}\in R^{n \times n} \qquad\qquad\qquad Equitation 7 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-55e036174315d76b63a5bff0cd71002d_l3.png)
![Rendered by QuickLaTeX.com \[ P_{x'}=\begin{bmatrix} w_{x'} &0& \ldots&0\\0&w_{x'}&\ldots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\ldots&w_{x'} \end{bmatrix}\in R^{n \times n} \qquad\qquad\qquad Equitation 8 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-e7a84435cc3da555a707654df9d97dc5_l3.png)
![Rendered by QuickLaTeX.com \[ P_{x''}=\begin{bmatrix} w_{x''}+\frac{w_{x'''}}{\Delta s^2} &0& \ldots&0&0\\[8pt]-\frac{2w_{x'''}}{\Delta s^2}&w_{x''}+\frac{2w_{x'''}}{\Delta s^2}&\ldots&0&0\\[8pt]\vdots&\vdots&\ddots&\vdots&\vdots\\[8pt]0&0&\ldots&w_{x''}+\frac{2w_{x'''}}{\Delta s^2}&0\\[8pt]0&0&\ldots&-\frac{2w_{x'''}}{\Delta s^2}&w_{x''}+\frac{w_{x'''}}{\Delta s^2} \end{bmatrix}\in R^{n \times n} \qquad\qquad\qquad Equitation 9 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-ebdafa8866c6ba3f6b250ec94e635f5a_l3.png)
![Rendered by QuickLaTeX.com \[ P=\begin{bmatrix} P_x &0&0\\0&P_{x'}&0\\0&0&P_{x''} \end{bmatrix}\in R^{3n \times 3n} \qquad\qquad\qquad Equitation 10 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-f8eec2dca715b6b29599cb4e7c7ab06f_l3.png)
![Rendered by QuickLaTeX.com \[ q=\begin{bmatrix} -r_0\\-r_1\\\vdots\\-r_{n-1}\\0\\\vdots\\0 \end{bmatrix}^T\in R^{1 \times 3n} \qquad\qquad\qquad Equitation 11 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-957d5fced4c0d4b2c804bfeca9c0b0b3_l3.png)
其中,公式6中从上到下依次对应![]() ,
, ![]() ,
, ![]() 。
。
这样代价函数![]() 就由上面的
就由上面的![]() ,
,![]() ,
,![]() 表示了。
表示了。
然后现在构建约束条件![]() :
:
frenet坐标系下,沿固定距离△s将路径均匀采样,使用常三阶多项式连接各个点(每段曲线的三阶导数jerk为常量):
![Rendered by QuickLaTeX.com \[ \begin{matrix} x_0\\x_0'\\x_0'' \end{matrix} \overset{\Dexta s}{\rightarrow} \begin{matrix} x_1\\x_1'\\x_1'' \end{matrix} \overset{\Dexta s}{\rightarrow} \begin{matrix} x_2\\x_2'\\x_2'' \end{matrix} ... \begin{matrix} x_{n-2}\\x_{n-2}'\\x_{n-2}'' \end{matrix} \overset{\Dexta s}{\rightarrow} \begin{matrix} x_{n-1}\\x_{n-1}'\\x_{n-1}'' \end{matrix} \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-7e28d0cade9dc7c8c21818f261faf9b4_l3.png)
得到:
![]()
![]()
![]()
![]()
将 ![]() 提取出来,可以得到:
提取出来,可以得到:
![]()
![]()
令
![]()
其中,公式18从上到下依次对应![]() ,
,![]() ,
,![]() 。
。
![]()
![]()
![Rendered by QuickLaTeX.com \[ A_{I}=\begin{bmatrix} -1 &1& 0&\ldots&0 \\0&-1&1&\ldots&0 \\\vdots&\vdots&\ddots&\ddots&\vdots \\0&0&\ldots&-1&1 \\0&0&\ldots&0&-1 \end{bmatrix}\in R^{n \times n} \qquad\qquad\qquad Equitation 21 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-9ec622e1aaaa09e835614cdb4ca4b7ff_l3.png)
![Rendered by QuickLaTeX.com \[ A=\begin{bmatrix} &A_x\\A_I&A_{ds}&A_{ds^2} \\0&A_I&A_{ds} \end{bmatrix}\in R^{5n \times 3n} \qquad\qquad\qquad Equitation 22 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-7fffdc5070946a5288c703a2dd71e78d_l3.png)
其中,公式22的第二行对应公式16,第三行对应公式17。
上下边界:
![Rendered by QuickLaTeX.com \[ l=\begin{bmatrix} x_{0l}\\[8pt]\vdots \\[8pt]x_{(n-1)l}\\[8pt]x'_{0l}\\[8pt]\vdots\\[8pt]x'_{(n-1)l}\\[8pt]x''_{0l}\\[8pt]\vdots\\[8pt]x''_{(n-1)l}\\[8pt]-\frac{\Delta s^3}{6}x'''_{bound}\\[8pt]\vdots\\[8pt]-\frac{\Delta s^3}{6}x'''_{bound}\\[8pt]-\frac{\Delta s^2}{2}x'''_{bound}\\[8pt]\vdots\\[8pt]-\frac{\Delta s^2}{2}x'''_{bound} \end{bmatrix}\in R^{5n \times 1} , u=\begin{bmatrix} x_{0u}\\[8pt]\vdots \\[8pt]x_{(n-1)u}\\[8pt]x'_{0u}\\[8pt]\vdots\\[8pt]x'_{(n-1)u}\\[8pt]x''_{0u}\\[8pt]\vdots\\[8pt]x''_{(n-1)u}\\[8pt]\frac{\Delta s^3}{6}x'''_{bound}\\[8pt]\vdots\\[8pt]\frac{\Delta s^3}{6}x'''_{bound}\\[8pt]\frac{\Delta s^2}{2}x'''_{bound}\\[8pt]\vdots\\[8pt]\frac{\Delta s^2}{2}x'''_{bound} \end{bmatrix}\in R^{5n \times 1} \qquad\qquad\qquad Equitation 23 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-d92708cbc74c49db7c300613ecf58642_l3.png)
Apollo代码的实现
PiecewiseJerkProblem::Optimize方法中,首先调用FormulateProblem()构造QP问题的Q,P和A,b,然后进行OSQP设置osqp_setup,最后调用osqp_solve求解。
bool PiecewiseJerkProblem::Optimize(const int max_iter) { OSQPData* data = FormulateProblem(); OSQPSettings* settings = SolverDefaultSettings(); settings->max_iter = max_iter; OSQPWorkspace* osqp_work = nullptr; osqp_work = osqp_setup(data, settings); // osqp_setup(&osqp_work, data, settings); osqp_solve(osqp_work); auto status = osqp_work->info->status_val; if (status < 0 || (status != 1 && status != 2)) { AERROR << "failed optimization status:\t" << osqp_work->info->status; osqp_cleanup(osqp_work); FreeData(data); c_free(settings); return false; } else if (osqp_work->solution == nullptr) { AERROR << "The solution from OSQP is nullptr"; osqp_cleanup(osqp_work); FreeData(data); c_free(settings); return false; } // extract primal results x_.resize(num_of_knots_); dx_.resize(num_of_knots_); ddx_.resize(num_of_knots_); for (size_t i = 0; i < num_of_knots_; ++i) { x_.at(i) = osqp_work->solution->x[i] / scale_factor_[0]; dx_.at(i) = osqp_work->solution->x[i + num_of_knots_] / scale_factor_[1]; ddx_.at(i) = osqp_work->solution->x[i + 2 * num_of_knots_] / scale_factor_[2]; } // Cleanup osqp_cleanup(osqp_work); FreeData(data); c_free(settings); return true; } |
其中,调用CalculateKernel进行P的构造,调用CalculateAffineConstraint进行A的构造,调用CalculateOffset进行Q的构造。
OSQPData* PiecewiseJerkProblem::FormulateProblem() { // calculate kernel std::vector<c_float> P_data; std::vector<c_int> P_indices; std::vector<c_int> P_indptr; CalculateKernel(&P_data, &P_indices, &P_indptr); // calculate affine constraints std::vector<c_float> A_data; std::vector<c_int> A_indices; std::vector<c_int> A_indptr; std::vector<c_float> lower_bounds; std::vector<c_float> upper_bounds; CalculateAffineConstraint(&A_data, &A_indices, &A_indptr, &lower_bounds, &upper_bounds); // calculate offset std::vector<c_float> q; CalculateOffset(&q); OSQPData* data = reinterpret_cast<OSQPData*>(c_malloc(sizeof(OSQPData))); CHECK_EQ(lower_bounds.size(), upper_bounds.size()); size_t kernel_dim = 3 * num_of_knots_; size_t num_affine_constraint = lower_bounds.size(); data->n = kernel_dim; data->m = num_affine_constraint; data->P = csc_matrix(kernel_dim, kernel_dim, P_data.size(), CopyData(P_data), CopyData(P_indices), CopyData(P_indptr)); data->q = CopyData(q); data->A = csc_matrix(num_affine_constraint, kernel_dim, A_data.size(), CopyData(A_data), CopyData(A_indices), CopyData(A_indptr)); data->l = CopyData(lower_bounds); data->u = CopyData(upper_bounds); return data; } |
构建P:
参见公式10。
void PiecewiseJerkPathProblem::CalculateKernel(std::vector<c_float>* P_data, std::vector<c_int>* P_indices, std::vector<c_int>* P_indptr) { const int n = static_cast<int>(num_of_knots_); const int num_of_variables = 3 * n; const int num_of_nonzeros = num_of_variables + (n - 1); std::vector<std::vector<std::pair<c_int, c_float>>> columns(num_of_variables); int value_index = 0; // x(i)^2 * (w_x + w_x_ref[i]), w_x_ref might be a uniform value for all x(i) // or piecewise values for different x(i) 参见公式7 for (int i = 0; i < n - 1; ++i) { columns[i].emplace_back(i, (weight_x_ + weight_x_ref_vec_[i]) / (scale_factor_[0] * scale_factor_[0])); ++value_index; } // x(n-1)^2 * (w_x + w_x_ref[n-1] + w_end_x) columns[n - 1].emplace_back( n - 1, (weight_x_ + weight_x_ref_vec_[n - 1] + weight_end_state_[0]) / (scale_factor_[0] * scale_factor_[0])); ++value_index; // x(i)'^2 * w_dx 参见公式8 for (int i = 0; i < n - 1; ++i) { columns[n + i].emplace_back( n + i, weight_dx_ / (scale_factor_[1] * scale_factor_[1])); ++value_index; } // x(n-1)'^2 * (w_dx + w_end_dx) columns[2 * n - 1].emplace_back(2 * n - 1, (weight_dx_ + weight_end_state_[1]) / (scale_factor_[1] * scale_factor_[1])); ++value_index; auto delta_s_square = delta_s_ * delta_s_; // x(i)''^2 * (w_ddx + 2 * w_dddx / delta_s^2) 参见公式9的对角线 columns[2 * n].emplace_back(2 * n, (weight_ddx_ + weight_dddx_ / delta_s_square) / (scale_factor_[2] * scale_factor_[2])); ++value_index; for (int i = 1; i < n - 1; ++i) { columns[2 * n + i].emplace_back( 2 * n + i, (weight_ddx_ + 2.0 * weight_dddx_ / delta_s_square) / (scale_factor_[2] * scale_factor_[2])); ++value_index; } columns[3 * n - 1].emplace_back( 3 * n - 1, (weight_ddx_ + weight_dddx_ / delta_s_square + weight_end_state_[2]) / (scale_factor_[2] * scale_factor_[2])); ++value_index; // -2 * w_dddx / delta_s^2 * x(i)'' * x(i + 1)'' 参见公式9的对角线下面的次对角线 for (int i = 0; i < n - 1; ++i) { columns[2 * n + i].emplace_back(2 * n + i + 1, (-2.0 * weight_dddx_ / delta_s_square) / (scale_factor_[2] * scale_factor_[2])); ++value_index; } CHECK_EQ(value_index, num_of_nonzeros); int ind_p = 0; for (int i = 0; i < num_of_variables; ++i) { P_indptr->push_back(ind_p); for (const auto& row_data_pair : columns[i]) { P_data->push_back(row_data_pair.second * 2.0); P_indices->push_back(row_data_pair.first); ++ind_p; } } P_indptr->push_back(ind_p); } |
构建Q:
参见公式11。
void PiecewiseJerkPathProblem::CalculateOffset(std::vector<c_float>* q) { CHECK_NOTNULL(q); const int n = static_cast<int>(num_of_knots_); const int kNumParam = 3 * n; q->resize(kNumParam, 0.0); if (has_x_ref_) { for (int i = 0; i < n; ++i) { q->at(i) += -2.0 * weight_x_ref_vec_.at(i) * x_ref_[i] / scale_factor_[0]; } } if (has_end_state_ref_) { q->at(n - 1) += -2.0 * weight_end_state_[0] * end_state_ref_[0] / scale_factor_[0]; q->at(2 * n - 1) += -2.0 * weight_end_state_[1] * end_state_ref_[1] / scale_factor_[1]; q->at(3 * n - 1) += -2.0 * weight_end_state_[2] * end_state_ref_[2] / scale_factor_[2]; } } |
构建A:
void PiecewiseJerkProblem::CalculateAffineConstraint( std::vector<c_float>* A_data, std::vector<c_int>* A_indices, std::vector<c_int>* A_indptr, std::vector<c_float>* lower_bounds, std::vector<c_float>* upper_bounds) { // 3N params bounds on x, x', x'' // 3(N-1) constraints on x, x', x'' // 3 constraints on x_init_ const int n = static_cast<int>(num_of_knots_); const int num_of_variables = 3 * n; const int num_of_constraints = num_of_variables + 3 * (n - 1) + 3; lower_bounds->resize(num_of_constraints); upper_bounds->resize(num_of_constraints); std::vector<std::vector<std::pair<c_int, c_float>>> variables( num_of_variables); int constraint_index = 0; // set x, x', x'' bounds 对应公式23的前3n行 for (int i = 0; i < num_of_variables; ++i) { if (i < n) { variables[i].emplace_back(constraint_index, 1.0); lower_bounds->at(constraint_index) = x_bounds_[i].first * scale_factor_[0]; upper_bounds->at(constraint_index) = x_bounds_[i].second * scale_factor_[0]; } else if (i < 2 * n) { variables[i].emplace_back(constraint_index, 1.0); lower_bounds->at(constraint_index) = dx_bounds_[i - n].first * scale_factor_[1]; upper_bounds->at(constraint_index) = dx_bounds_[i - n].second * scale_factor_[1]; } else { variables[i].emplace_back(constraint_index, 1.0); lower_bounds->at(constraint_index) = ddx_bounds_[i - 2 * n].first * scale_factor_[2]; upper_bounds->at(constraint_index) = ddx_bounds_[i - 2 * n].second * scale_factor_[2]; } ++constraint_index; } CHECK_EQ(constraint_index, num_of_variables); // x(i->i+1)''' = (x(i+1)'' - x(i)'') / delta_s 对应公式12 for (int i = 0; i + 1 < n; ++i) { variables[2 * n + i].emplace_back(constraint_index, -1.0); variables[2 * n + i + 1].emplace_back(constraint_index, 1.0); lower_bounds->at(constraint_index) = dddx_bound_.first * delta_s_ * scale_factor_[2]; upper_bounds->at(constraint_index) = dddx_bound_.second * delta_s_ * scale_factor_[2]; ++constraint_index; } // x(i+1)' - x(i)' - 0.5 * delta_s * x(i)'' - 0.5 * delta_s * x(i+1)'' = 0 对应公式17 for (int i = 0; i + 1 < n; ++i) { variables[n + i].emplace_back(constraint_index, -1.0 * scale_factor_[2]); variables[n + i + 1].emplace_back(constraint_index, 1.0 * scale_factor_[2]); variables[2 * n + i].emplace_back(constraint_index, -0.5 * delta_s_ * scale_factor_[1]); variables[2 * n + i + 1].emplace_back(constraint_index, -0.5 * delta_s_ * scale_factor_[1]); lower_bounds->at(constraint_index) = 0.0; upper_bounds->at(constraint_index) = 0.0; ++constraint_index; } // x(i+1) - x(i) - delta_s * x(i)' // - 1/3 * delta_s^2 * x(i)'' - 1/6 * delta_s^2 * x(i+1)'' 对应公式16 auto delta_s_sq_ = delta_s_ * delta_s_; for (int i = 0; i + 1 < n; ++i) { variables[i].emplace_back(constraint_index, -1.0 * scale_factor_[1] * scale_factor_[2]); variables[i + 1].emplace_back(constraint_index, 1.0 * scale_factor_[1] * scale_factor_[2]); variables[n + i].emplace_back( constraint_index, -delta_s_ * scale_factor_[0] * scale_factor_[2]); variables[2 * n + i].emplace_back( constraint_index, -delta_s_sq_ / 3.0 * scale_factor_[0] * scale_factor_[1]); variables[2 * n + i + 1].emplace_back( constraint_index, -delta_s_sq_ / 6.0 * scale_factor_[0] * scale_factor_[1]); lower_bounds->at(constraint_index) = 0.0; upper_bounds->at(constraint_index) = 0.0; ++constraint_index; } // constrain on x_init variables[0].emplace_back(constraint_index, 1.0); lower_bounds->at(constraint_index) = x_init_[0] * scale_factor_[0]; upper_bounds->at(constraint_index) = x_init_[0] * scale_factor_[0]; ++constraint_index; variables[n].emplace_back(constraint_index, 1.0); lower_bounds->at(constraint_index) = x_init_[1] * scale_factor_[1]; upper_bounds->at(constraint_index) = x_init_[1] * scale_factor_[1]; ++constraint_index; variables[2 * n].emplace_back(constraint_index, 1.0); lower_bounds->at(constraint_index) = x_init_[2] * scale_factor_[2]; upper_bounds->at(constraint_index) = x_init_[2] * scale_factor_[2]; ++constraint_index; CHECK_EQ(constraint_index, num_of_constraints); int ind_p = 0; for (int i = 0; i < num_of_variables; ++i) { A_indptr->push_back(ind_p); for (const auto& variable_nz : variables[i]) { // coefficient A_data->push_back(variable_nz.second); // constraint index A_indices->push_back(variable_nz.first); ++ind_p; } } // We indeed need this line because of // https://github.com/oxfordcontrol/osqp/blob/master/src/cs.c#L255 A_indptr->push_back(ind_p); } |
Python代码的实现
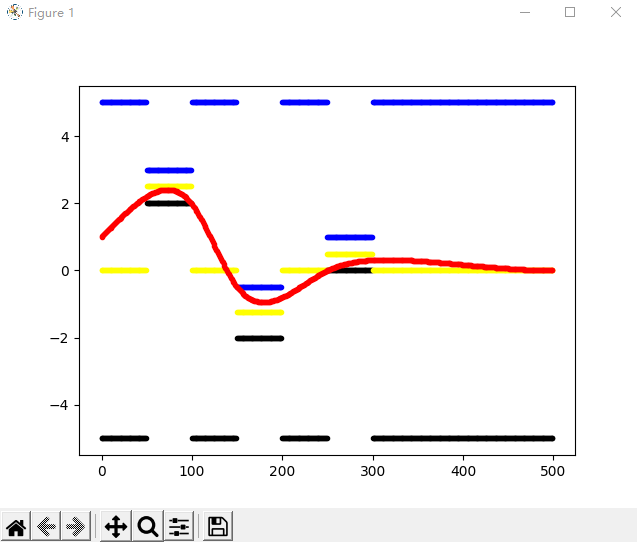
import matplotlib.pyplot as plt import osqp import numpy as np from scipy import sparse import random # 障碍物设置 obs = [[5, 10, 2, 3], [15, 20, -2, -0.5], [25, 30, 0, 1]] # start_s,end_s,l_low,l_up s_len = 50 delta_s = 0.1 n = int(s_len / delta_s) x = np.linspace(0, s_len, n) up_bound = [0] * (5 * n + 3) low_bound = [0] * (5 * n + 3) s_ref = [0] * 3 * n dddl_bound = 0.01 ####################边界提取################ l_bound = 5 for i in range(n): for j in range(len(obs)): if x[i] >= obs[j][0] and x[i] <= obs[j][1]: low_ = obs[j][2] up_ = obs[j][3] break else: up_ = l_bound low_ = -l_bound up_bound[i] = up_ low_bound[i] = low_ s_ref[i] = 0.5 * (up_ + low_) for i in range(3 * n, 4 * n): up_bound[i] = dddl_bound * delta_s * delta_s * delta_s / 6 low_bound[i] = -dddl_bound * delta_s * delta_s * delta_s / 6 for i in range(4 * n, 5 * n): up_bound[i] = dddl_bound * delta_s * delta_s / 2 low_bound[i] = -dddl_bound * delta_s * delta_s / 2 ####################构造P和Q################ w_l = 0.005 w_dl = 1 w_ddl = 1 w_dddl = 0.1 eye_n = np.identity(n) zero_n = np.zeros((n, n)) P_zeros = zero_n P_l = w_l * eye_n P_dl = w_dl * eye_n P_ddl = (w_ddl + 2 * w_dddl / delta_s / delta_s) * eye_n - 2 * w_dddl / delta_s / delta_s * np.eye(n, k=-1) P_ddl[0][0] = w_ddl + w_dddl / delta_s / delta_s P_ddl[n - 1][n - 1] = w_ddl + w_dddl / delta_s / delta_s P = sparse.csc_matrix(np.block([ [P_l, P_zeros, P_zeros], [P_zeros, P_dl, P_zeros], [P_zeros, P_zeros, P_ddl] ])) q = np.array([-w_l * s_ for s_ in s_ref]) ####################构造A和LU################ # 构造:l(i+1) = l(i) + l'(i) * delta_s + 1/2 * l''(i) * delta_s^2 + 1/6 * l'''(i) * delta_s^3 A_ll = -eye_n + np.eye(n, k=1) A_ldl = -delta_s * eye_n A_lddl = -0.5 * delta_s * delta_s * eye_n A_l = (np.block([ [A_ll, A_ldl, A_lddl] ])) # 构造:l'(i+1) = l'(i) + l''(i) * delta_s + 1/2 * l'''(i) * delta_s^2 A_dll = zero_n A_dldl = -eye_n + np.eye(n, k=1) A_dlddl = -delta_s * eye_n A_dl = np.block([ [A_dll, A_dldl, A_dlddl] ]) A_ul = np.block([ [eye_n, zero_n, zero_n], [zero_n, zero_n, zero_n], [zero_n, zero_n, zero_n] ]) # 3n*3n # 初始化设置 A_init = np.zeros((3, 3 * n)) A_init[0][0] = 1 A = sparse.csc_matrix(np.row_stack((A_ul, A_l, A_dl, A_init))) low_bound[5 * n] = 1 up_bound[5 * n] = 1 l = np.array(low_bound) u = np.array(up_bound) # Create an OSQP object prob = osqp.OSQP() # Setup workspace and change alpha parameter prob.setup(P, q, A, l, u, alpha=1.0) # Solve problem res = prob.solve() plt.plot(u[:n], '.', color='blue') plt.plot(l[:n], '.', color='black') plt.plot(s_ref[:n],'.', color='yellow') plt.plot(res.x[:n], '.', color='red') plt.show() |
参考文献
规划控制:Piecewise Jerk Path Optimizer的python实现
Apollo 6.0 QP(二次规划)算法解析
Piecewise Jerk Path Optimizer
本作品采用知识共享署名 4.0 国际许可协议进行许可。