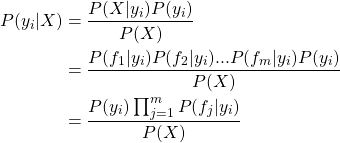引言
随机森林算法是机器学习等领域里的一个比较广泛的算法,它可以用来分类,回归等。随机森林由多个决策树组成,相对单个决策树算法,其效果更好,且不容易出现过度拟合。
其一般构建方法为:
1 构建几棵决策树树,使用装袋方法,用泊松分布或伯努力分布对样本进行分配到每棵树上。
2 从每棵树的根节点开始对属性(feature)进行分割
3 对每个分割点,找到最好的分割方式,把记录分成左右两个子节点,即哪个feature可以更好地使记录最纯,其中每个feature的所有分割点中总会有一个点是记录更纯。一般左子节点比右子节点纯。所谓最纯,就是说所有的数据按这个属性分割后无法用其它属性再分割。
4 子节点如果已最纯,就停止继续分割,否则继续以子节点为当前的根节点按照2,3步骤继续分割。
目前有3种纯度计算公式,Gini,Entropy熵和错误率:
![Rendered by QuickLaTeX.com \[ Gini = 1 - \sum_{i=1}^n P(i)^2 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-68071edc5bc54c6477160dab233226ae_l3.png)
![Rendered by QuickLaTeX.com \[ Entropy = - \sum_{i=1}^n P(i) * log_2^{P(i)} \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-9cba594a3e8f66458c1f0122da6ef0bd_l3.png)
![Rendered by QuickLaTeX.com \[ Error = 1 - max P(i), i \in [1,n] \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-ce1422582a4c07f411e4d864fafd82bb_l3.png)
下面以Spark中的一个随机森林的单元测试代码为例分析随机森林模型的构建。
构建随机森林
test("alternating categorical and continuous features with multiclass labels to test indexing") {
val arr = Array(
LabeledPoint(0.0, Vectors.dense(1.0, 0.0, 0.0, 3.0, 1.0)), //A
LabeledPoint(1.0, Vectors.dense(0.0, 1.0, 1.0, 1.0, 2.0)), //B
LabeledPoint(0.0, Vectors.dense(2.0, 0.0, 0.0, 6.0, 3.0)), //C
LabeledPoint(2.0, Vectors.dense(0.0, 2.0, 1.0, 3.0, 2.0)) //D
)
val rdd = sc.parallelize(arr)
val categoricalFeatures = Map(0 -> 3, 2 -> 2, 4 -> 4)
val numClasses = 3
val rf = new RandomForestClassifier()
.setImpurity("Gini")
.setMaxDepth(5)
.setNumTrees(2)
.setFeatureSubsetStrategy("sqrt")
.setSeed(12345)
compareAPIs(rdd, rf, categoricalFeatures, numClasses)
} |
test("alternating categorical and continuous features with multiclass labels to test indexing") {
val arr = Array(
LabeledPoint(0.0, Vectors.dense(1.0, 0.0, 0.0, 3.0, 1.0)), //A
LabeledPoint(1.0, Vectors.dense(0.0, 1.0, 1.0, 1.0, 2.0)), //B
LabeledPoint(0.0, Vectors.dense(2.0, 0.0, 0.0, 6.0, 3.0)), //C
LabeledPoint(2.0, Vectors.dense(0.0, 2.0, 1.0, 3.0, 2.0)) //D
)
val rdd = sc.parallelize(arr)
val categoricalFeatures = Map(0 -> 3, 2 -> 2, 4 -> 4)
val numClasses = 3
val rf = new RandomForestClassifier()
.setImpurity("Gini")
.setMaxDepth(5)
.setNumTrees(2)
.setFeatureSubsetStrategy("sqrt")
.setSeed(12345)
compareAPIs(rdd, rf, categoricalFeatures, numClasses)
}
上面的测试数据中,共有3个分类(class):0.0 1.0 2.0,共有5个属性(feature),
其中3个为非连续属性,feature 0可分割为3类,feature 2可分割为2类,feature 4可分割为4类。
后续的代码对连续属性分类后,可得到属性的分割点如下:
0: 0 1 2
1: 0 1 2 //连续属性分割结果
2: 0 //只有2个属性,转换为2分类属性,即用boolean表示即可
3: 1 3 6 //连续属性分割结果
4: 0 1 2 3
按照属性的分割点进行索引,样本可表示为:
A LabeledPoint(0.0, Vectors.dense(1.0, 0.0, 0.0, 3.0, 1.0)), 1 0 0 1 1
B LabeledPoint(1.0, Vectors.dense(0.0, 1.0, 1.0, 1.0, 2.0)), 0 1 1 0 2
C LabeledPoint(0.0, Vectors.dense(2.0, 0.0, 0.0, 6.0, 3.0)), 2 0 0 2 3
D LabeledPoint(2.0, Vectors.dense(0.0, 2.0, 1.0, 3.0, 2.0)) 0 2 1 1 2
下面代码抽样装袋后,本例可以构建为如下2棵树:(抽样的一种结果,其中tree1的3个feature和tree2的3个feature也是随机选择的)
tree 1(feature:0 1 3) tree 0(feature:0 1 4)
node 1(node index:0) node 1(node index:1)
样本 B A 3次B样本
feature0 010 000 000 030 100 000
feature1 000 010 000 100 030 000
feature2
feature3 010 000 000
feature4 000 100 030 000
上面的010 000 000等数据是DTStatsAggregator类中的allStats变量的值。
tree 1中allStats的数据可解读为feature 0, feature 1和feature 3顺序排列,各占9位。
每个feature含有3个bin(桶)(属性分割后),每个bin有3位,分别记录3个分类的数量。
如feature0 010 000 000理解为feature 0的第0个bin的分类1有1个样本。
如feature4 000 100 030 000理解为feature 4的第1个bin的分类0有1个样本,第2个bin的分类1有3个样本。
这些都是根据输入样本统计出的结果。
继续阅读“Random Forest(随机森林) in ML”本作品采用知识共享署名 4.0 国际许可协议进行许可。
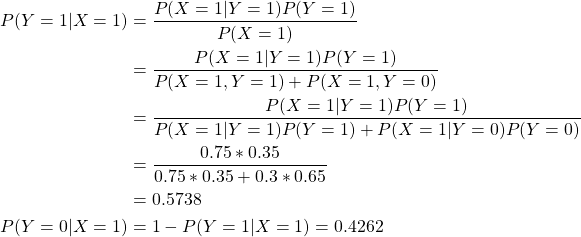
![Rendered by QuickLaTeX.com \[ P(X|Y=y) = \prod_{i=1}^d P(X_i|Y=y) \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-46d41c8f727e5d51803e08a400dd7359_l3.png)