分类： Tensorflow

卷积神经网络（CNN）是指在所有网络中，至少优一层使用了卷积运算运算的神经网络，因此命名为卷积神经网络。
那么什么是卷积呢？如果需要卷积一个二位图片，首先定义一个卷积核（kernel），即权重矩阵，它能表面每一次卷积那个方向的值更重要，然后逐步在二维输入数据上“扫描卷积”。当卷积核“滑动”的同时进行卷积：计算权重矩阵和扫描所得的数据矩阵的乘积，求和后得到一个像素输出。
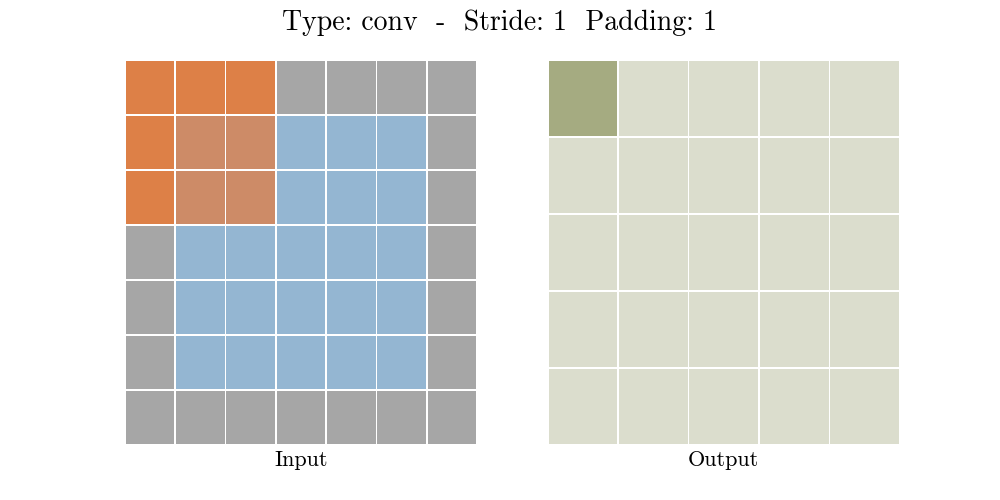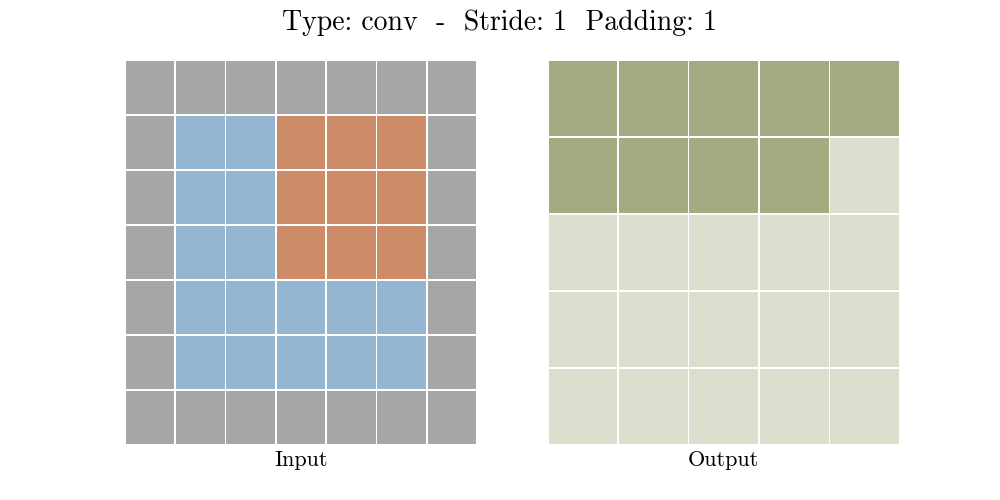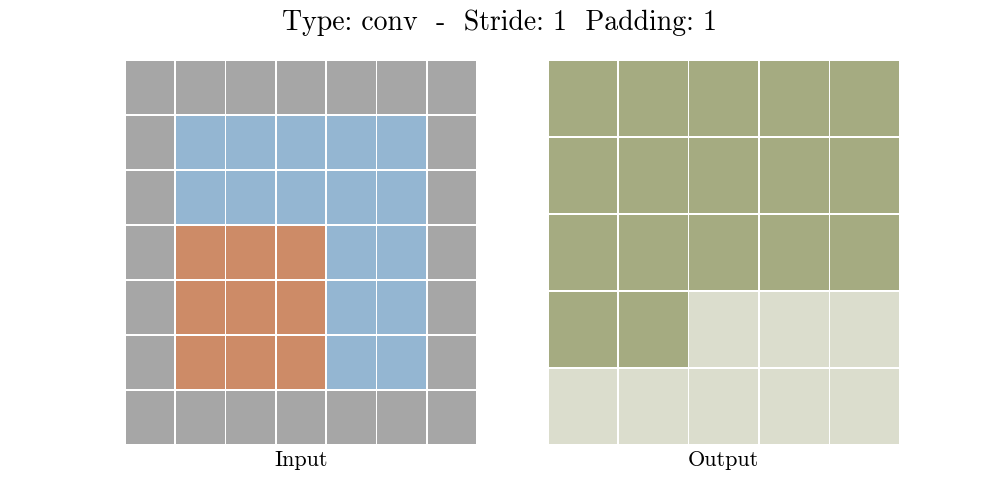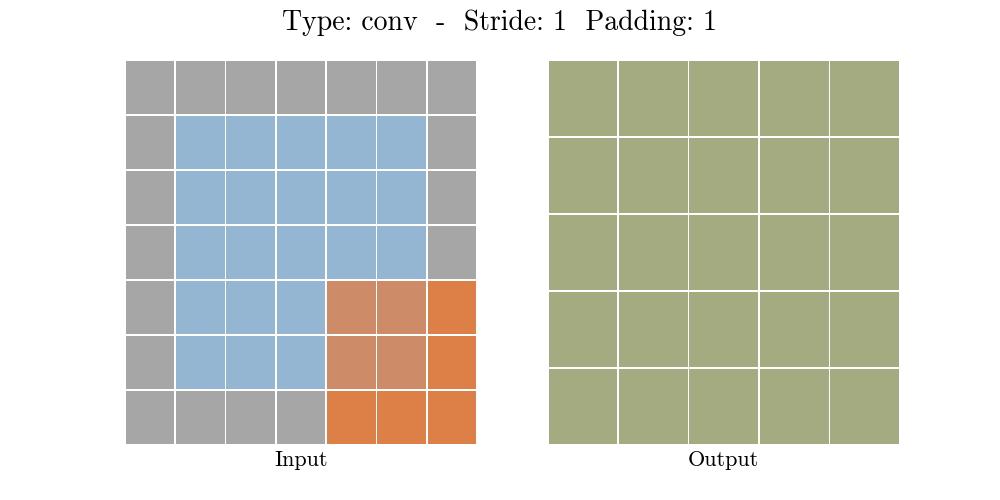
步长（Stride）为每次卷积核移动格数，填充（Padding）为是否对元素数据进行边缘填充。当不填充的时候，即Tensorflow中的VALID选项，卷积后的数据会比输入数据小，而加入合适的填充后，即Tensorflow中的SAME选项，卷积后的数据可以保持和输入数据大小一致。如下图所示：

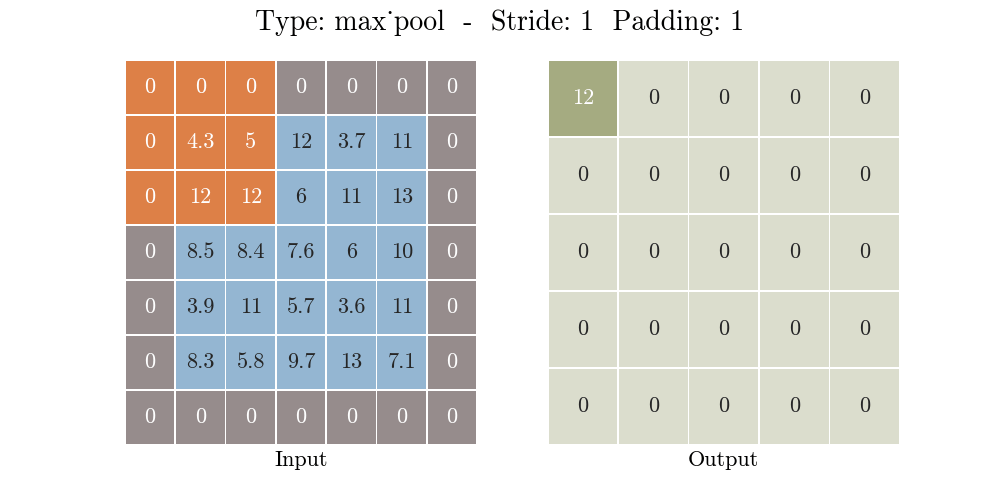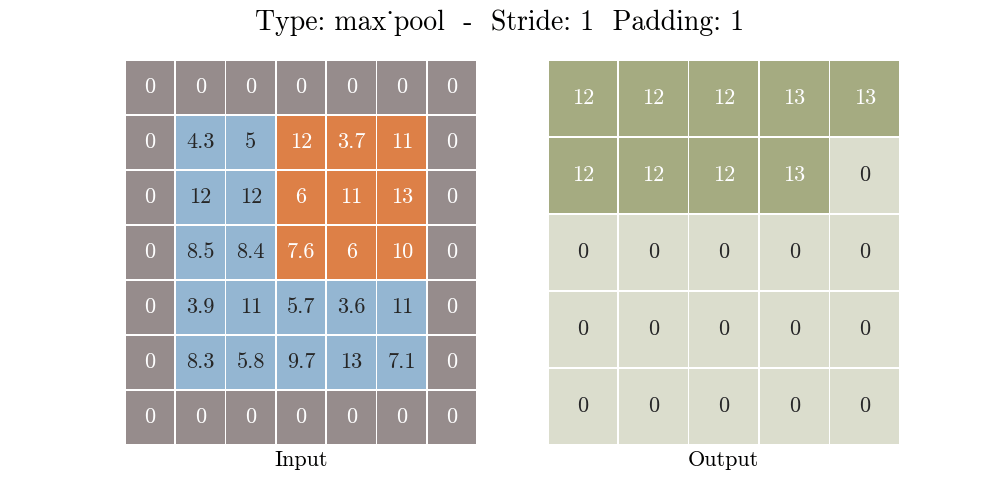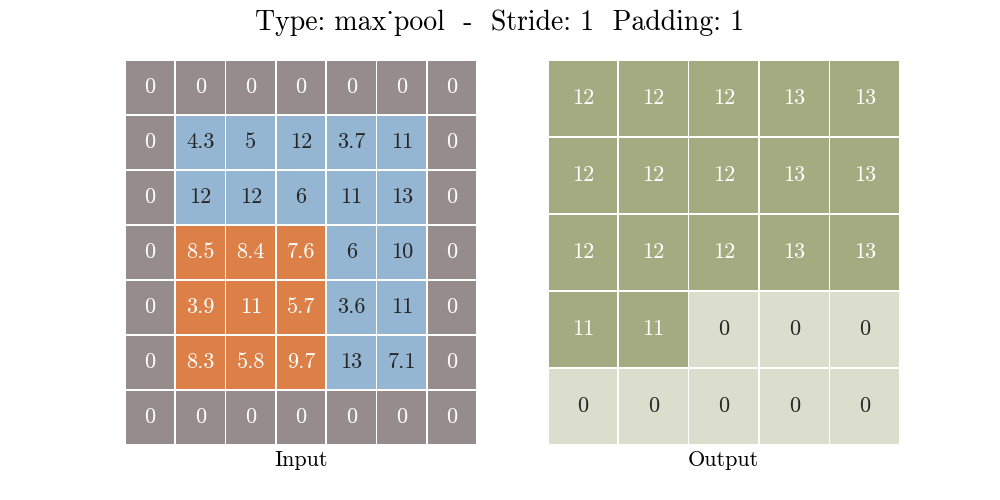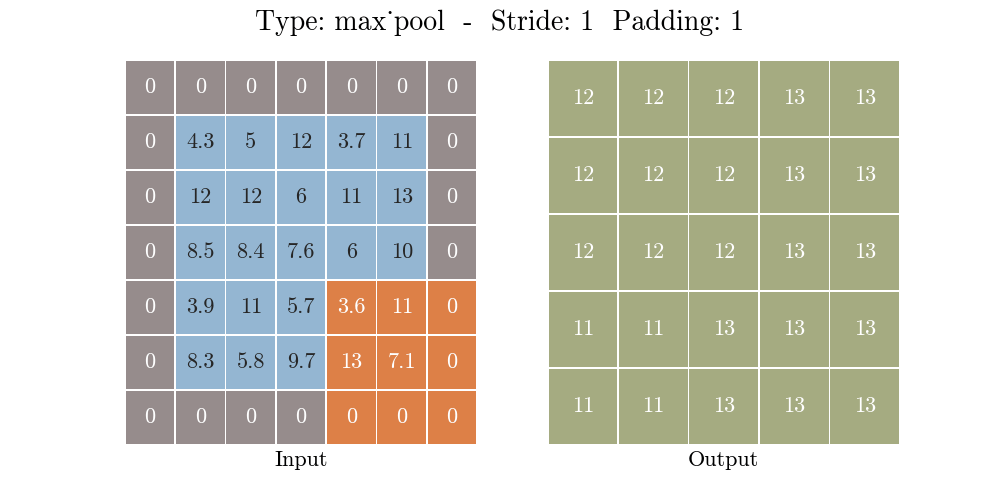
那么什么是池化呢？池化也称为欠采样或下采样。主要用于特征降维，在保持旋转、平移、伸缩等不变性的前提下，压缩数据和参数的数量，减小过拟合，同时提高模型的容错性。常用的有按均值池化（mean-pooling）：更大地保留图像背景信息，按最大值池化（max-pooling）：更多的保留纹理信息。如下图所示，池化大大压缩了数据：

原理

以下面的测试程序来讨论Conv2D（卷积）和MaxPool2D（池化）的具体实现原理：
首先定义一个具有1张图，大小为6X6，通道为1个，即输入数据img的shape为[1,6,6,1]。
然后定义过滤器filter，NHWC格式，即批次，高，宽，通道格式，和输入数据是同一个格式。
下图为不同的卷积核对同一图片处理的结果：

测试程序

如下程序和图片示例，一个 3X3 的filter（卷积核的特征是提取图片从左上到右下的特征）在 6X6 的图片上，按照步长 1X1 从左往右，从上往下计算蒙版区域输出结果。
卷积计算：
图例1的卷积计算为：1*1 + 0*-1 + 0*-1 + 0*-1 + 1*1 + 0*-1 + 0*-1 + 0*-1 + 1*1 = 3
图例2的卷积计算为：1*1 + 0*-1 + 0*-1 + 0*-1 + 1*1 + 1*-1 + 0*-1 + 0*-1 + 0*1 = 1

继续阅读“Tensorflow Conv2D和MaxPool2D原理”本作品采用知识共享署名 4.0 国际许可协议进行许可。

实例学习

了解上文的Embedding和Pooling原理后，就可以理解Tensorflow的示例程序了：
1 加载测试数据IMDB imdb；
2 对每个样本进行padding操作，补齐到256长的数组（keras.preprocessing.sequence.pad_sequences），完成后为 mX256 的矩阵；
3 创建模型，先使用Embedding把输入的稀疏矩阵进行致密矩阵的映射，完成后为 mX256X16 的矩阵；
4 然后进行Pooling把矩阵降维，完成后为 mX16 的矩阵；
5 最后进行2个全连接操作，完成后分别为 mX16，mX1 的矩阵，由此得到每条评论的结果，好评或差评；
6 通过训练完成神经元参数的设置，然后可以对测试数据进行分类。
继续阅读“Tensorflow 文本分类实例”本作品采用知识共享署名 4.0 国际许可协议进行许可。

池化（Pooling）：也称为欠采样或下采样。主要用于特征降维，在保持旋转、平移、伸缩等不变性的前提下，压缩数据和参数的数量，减小过拟合，同时提高模型的容错性。常用的有按均值池化（mean-pooling）：更大地保留图像背景信息，按最大值池化（max-pooling）：更多的保留纹理信息。

池化原理

Tensorflow的池化(pooling.py)API主要包括1D，2D和3D的平均池化和最大池化。
平均池化通过API math_ops.reduce_mean 完成，最大池化通过API math_ops.reduce_max完成。

测试程序

以下面程序为例（这儿是GlobalMaxPooling2D）：
继续阅读“Tensorflow Pooling池化原理”本作品采用知识共享署名 4.0 国际许可协议进行许可。

Embedding（嵌入）指的是把低维的流形嵌入到高维空间中。举个简单的例子，三维空间的球体（地球）是一个二维流形嵌入在三维空间（欧几里得空间），即地球上的任意一个点只需一个二维的经纬度就可以表达，但三维空间中用x,y,z。深度学习领域假设“自然的原始数据是低维的流形嵌入到原始数据所在的高维空间中”。所以，深度学习的过程就是把高维原始数据（图像，句子）再回映射到低维流形中，从而是数据变得可分，而这个映射就叫嵌入（Embedding）。比如文档Embedding，就是把每篇文档所组成的单词映射到一个低维的表征向量，使得每篇文档可以用一个表征向量来表示，即Embedding就是从原始数据提取出来的Feature，也就是通过神经网络映射之后的低维向量。
如下例子，蓝色曲线和红色曲线是无法线性可分的（图二），只能用非线性函数分离（图三），但真实的数据中却很难找到这样的非线性函数，但通过对数据进行Embedding过程进行映射后（图四），就可以线性可分了。

文档Embedding原理

在对文本进行分类的过程中，第一步便是需要对文本样本进行降维，比如文本字库大小为10000，不能用10000列队矩阵来进行全连接计算，由于每个样本大概只占300个单词的稀疏向量，所以我们可以用一个列数更少的致密向量来代替每个样本，即可以用300个Embedding向量来对所有的文档进行低维映射。
Embedding方法就是用来把文本样本的稀疏矩阵转换为致密矩阵的一个方法。

假设有如下的矩阵乘法：
一个由m个文本样本，每个样本由n个特征构成的稀疏向量，组成的样本库。每个样本中含有的单词用1表示，比如第一个样本有2个单词。
现在构建一个Embedding矩阵，大小为n * k。其中Embedding矩阵的值可以用uniform方法进行随机初始化。
用样本中对应1的位置进行Embedding向量选择，然后相加，得到最终的向量 [5 7 9 11]。这样，m * n 的稀疏矩阵就变成了 m * k 的致密矩阵了。

继续阅读“Tensorflow Embedding原理”本作品采用知识共享署名 4.0 国际许可协议进行许可。

本文通过一个简单的程序来验证Tensorflow能够进行函数式编程的底层支持。从此也说明，Tensorflow在2.0发布之前的1.15版本底层已经支持函数式编程，进而能够实现动态图计算。
回目录

函数式编程测试程序

如下验证了用Tensorflow的函数式编程实现如下代码逻辑：

int feed1 = 2;
int feed2 = 10;
int feed3 = 3;
while( feed1 < feed2 ){
  feed1 = feed1 + 3;
}
feed1 = feed1 + feed3

继续阅读“Tensorflow 函数式编程的测试”本作品采用知识共享署名 4.0 国际许可协议进行许可。