G2O是一个开源的C++框架,用于优化基于图形的非线性误差函数。g2o被设计为易于扩展到各种各样的问题,一个新的问题通常可以在几行代码中指定。
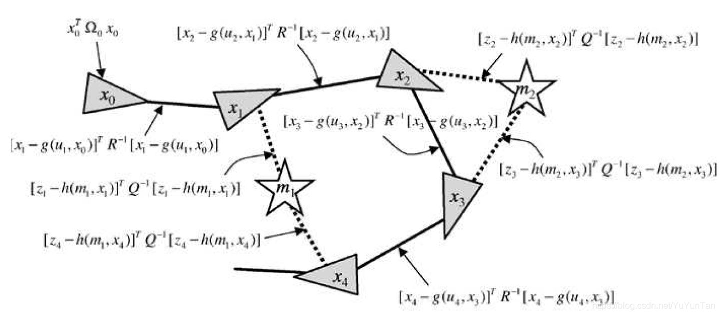
当前的实现为SLAM和BA的几个变体提供了解决方案,机器人技术和计算机视觉中的一系列问题都涉及到最小化可以用图形表示的非线性误差函数,典型的例子是同步定位和映射(SLAM)或束调整(BA)。这些问题的总体目标是最大限度地找到能够解释受到高斯噪声影响后的一组测量数据的参数或状态变量的配置。通过把优化问题设计成图的模式:带优化的变量称为顶点,对于待优量的限制条件为边。限制条件可理解成损失函数,这个函数是优化的关键,我们要通过不断的迭代获取最小的损失,从而推断出优化后的顶点而求解。
G2O是一个开源的C++框架,用于解决非线性最小二乘问题。G2O的性能可与针对特定问题的最先进方法的实现相媲美。本文通过曲线上的点受高斯噪声影响后,利用G2O设计图模型,然后经过手动计算微分实现来重新拟合曲线。
接上篇
非线性优化,接着解析G2O框架对非线性优化的实现,本文的微分计算为手动微分。
上篇多项式方程的G2O优化方式代码:
#include <iostream>
#include <g2o/core/g2o_core_api.h>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/core/optimization_algorithm_dogleg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <g2o/stuff/sampler.h>
#include <Eigen/Core>
#include <cmath>
#include <chrono>
using namespace std;
// 曲线模型的顶点,模板参数:优化变量维度和数据类型
class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
// 重置
virtual void setToOriginImpl() override {
_estimate << 0, 0, 0;
}
// 更新,每一轮迭代后更新参数的值Δx。
virtual void oplusImpl(const double *update) override {
_estimate += Eigen::Vector3d(update);
}
// 存盘和读盘:留空
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
};
// 误差模型 模板参数:观测值维度,类型,连接顶点类型
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
// 计算曲线模型误差,测量值减去估计值得到误差。
virtual void computeError() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
_error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
}
// 计算雅可比矩阵,和上一篇高斯牛顿法里面的求解方式是一样的。
virtual void linearizeOplus() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
_jacobianOplusXi[0] = -_x * _x * y;
_jacobianOplusXi[1] = -_x * y;
_jacobianOplusXi[2] = -y;
}
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
public:
double _x; // x 值, y 值为 _measurement
};
int main(int argc, char **argv) {
double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值
double ae = 2.0, be = -1.0, ce = 5.0; // 估计参数值
int N = 100; // 数据点
double w_sigma = 1.0; // 噪声Sigma值
double inv_sigma = 1.0 / w_sigma;
g2o::Sampler::seedRand();
vector<double> x_data, y_data; // 数据
for (int i = 0; i < N; i++) {
double x = i / 100.0;
x_data.push_back(x);
y_data.push_back(exp(ar * x * x + br * x + cr) + g2o::Sampler::gaussRand(0, 0.02));//加上一个高斯误差,来表示测量是不准确的。
}
// 构建图优化,先设定g2o
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType; // 每个误差项优化变量维度为3,误差值维度为1
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
// 梯度下降方法,可以从GN, LM, DogLeg 中选
auto solver = new g2o::OptimizationAlgorithmGaussNewton(
g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
// 往图中增加顶点:待优化的参数。
//图优化的原理就是:不停的调整顶点位姿(参数)来使连接到顶点的边(误差函数)最优。
CurveFittingVertex *v = new CurveFittingVertex();
v->setEstimate(Eigen::Vector3d(ae, be, ce));
v->setId(0);
optimizer.addVertex(v);
// 往图中增加边:每个误差函数
for (int i = 0; i < N; i++) {
CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
edge->setId(i);
edge->setVertex(0, v); // 设置连接的顶点
edge->setMeasurement(y_data[i]); // 观测数值
// 信息矩阵:协方差矩阵之逆,乘上一阶导数值用来决定当前梯度对全局梯度的贡献度。信息越清晰表明当前梯度越重要。
// 即人为的根据先验概率控制误差函数的权重。
edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma));
optimizer.addEdge(edge);
}
// 执行优化
cout << "start optimization" << endl;
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
optimizer.initializeOptimization();
optimizer.optimize(10);
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
// 输出优化值
Eigen::Vector3d abc_estimate = v->estimate();
cout << "estimated model: " << abc_estimate.transpose() << endl;
return 0;
} |
#include <iostream>
#include <g2o/core/g2o_core_api.h>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/core/optimization_algorithm_dogleg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <g2o/stuff/sampler.h>
#include <Eigen/Core>
#include <cmath>
#include <chrono>
using namespace std;
// 曲线模型的顶点,模板参数:优化变量维度和数据类型
class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
// 重置
virtual void setToOriginImpl() override {
_estimate << 0, 0, 0;
}
// 更新,每一轮迭代后更新参数的值Δx。
virtual void oplusImpl(const double *update) override {
_estimate += Eigen::Vector3d(update);
}
// 存盘和读盘:留空
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
};
// 误差模型 模板参数:观测值维度,类型,连接顶点类型
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
// 计算曲线模型误差,测量值减去估计值得到误差。
virtual void computeError() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
_error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
}
// 计算雅可比矩阵,和上一篇高斯牛顿法里面的求解方式是一样的。
virtual void linearizeOplus() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
_jacobianOplusXi[0] = -_x * _x * y;
_jacobianOplusXi[1] = -_x * y;
_jacobianOplusXi[2] = -y;
}
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
public:
double _x; // x 值, y 值为 _measurement
};
int main(int argc, char **argv) {
double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值
double ae = 2.0, be = -1.0, ce = 5.0; // 估计参数值
int N = 100; // 数据点
double w_sigma = 1.0; // 噪声Sigma值
double inv_sigma = 1.0 / w_sigma;
g2o::Sampler::seedRand();
vector<double> x_data, y_data; // 数据
for (int i = 0; i < N; i++) {
double x = i / 100.0;
x_data.push_back(x);
y_data.push_back(exp(ar * x * x + br * x + cr) + g2o::Sampler::gaussRand(0, 0.02));//加上一个高斯误差,来表示测量是不准确的。
}
// 构建图优化,先设定g2o
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType; // 每个误差项优化变量维度为3,误差值维度为1
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
// 梯度下降方法,可以从GN, LM, DogLeg 中选
auto solver = new g2o::OptimizationAlgorithmGaussNewton(
g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
// 往图中增加顶点:待优化的参数。
//图优化的原理就是:不停的调整顶点位姿(参数)来使连接到顶点的边(误差函数)最优。
CurveFittingVertex *v = new CurveFittingVertex();
v->setEstimate(Eigen::Vector3d(ae, be, ce));
v->setId(0);
optimizer.addVertex(v);
// 往图中增加边:每个误差函数
for (int i = 0; i < N; i++) {
CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
edge->setId(i);
edge->setVertex(0, v); // 设置连接的顶点
edge->setMeasurement(y_data[i]); // 观测数值
// 信息矩阵:协方差矩阵之逆,乘上一阶导数值用来决定当前梯度对全局梯度的贡献度。信息越清晰表明当前梯度越重要。
// 即人为的根据先验概率控制误差函数的权重。
edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma));
optimizer.addEdge(edge);
}
// 执行优化
cout << "start optimization" << endl;
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
optimizer.initializeOptimization();
optimizer.optimize(10);
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
// 输出优化值
Eigen::Vector3d abc_estimate = v->estimate();
cout << "estimated model: " << abc_estimate.transpose() << endl;
return 0;
}
调用优化器对图进行优化:
int SparseOptimizer::optimize(int iterations, bool online)
{//没有顶点,退出
if (_ivMap.size() == 0) {
cerr << __PRETTY_FUNCTION__ << ": 0 vertices to optimize, maybe forgot to call initializeOptimization()" << endl;
return -1;
}
int cjIterations=0;
number_t cumTime=0;
bool ok=true;
ok = _algorithm->init(online);
if (! ok) {
cerr << __PRETTY_FUNCTION__ << " Error while initializing" << endl;
return -1;
}
_batchStatistics.clear();
if (_computeBatchStatistics)
_batchStatistics.resize(iterations);
OptimizationAlgorithm::SolverResult result = OptimizationAlgorithm::OK;
//循环开始每一轮优化
for (int i=0; i<iterations && ! terminate() && ok; i++){
preIteration(i);
if (_computeBatchStatistics) {
G2OBatchStatistics& cstat = _batchStatistics[i];
G2OBatchStatistics::setGlobalStats(&cstat);
cstat.iteration = i;
cstat.numEdges = _activeEdges.size();
cstat.numVertices = _activeVertices.size();
}
number_t ts = get_monotonic_time();
//调用求解器,求解此轮Δx的值
result = _algorithm->solve(i, online);
ok = ( result == OptimizationAlgorithm::OK );
bool errorComputed = false;
if (_computeBatchStatistics) {
computeActiveErrors();
errorComputed = true;
_batchStatistics[i].chi2 = activeRobustChi2();
_batchStatistics[i].timeIteration = get_monotonic_time()-ts;
}
if (verbose()){
number_t dts = get_monotonic_time()-ts;
cumTime += dts;
if (! errorComputed)
computeActiveErrors();
cerr << "iteration= " << i
<< "\t chi2= " << FIXED(activeRobustChi2())
<< "\t time= " << dts
<< "\t cumTime= " << cumTime
<< "\t edges= " << _activeEdges.size();
_algorithm->printVerbose(cerr);
cerr << endl;
}
++cjIterations;
postIteration(i);
}
if (result == OptimizationAlgorithm::Fail) {
return 0;
}
return cjIterations;
} |
int SparseOptimizer::optimize(int iterations, bool online)
{//没有顶点,退出
if (_ivMap.size() == 0) {
cerr << __PRETTY_FUNCTION__ << ": 0 vertices to optimize, maybe forgot to call initializeOptimization()" << endl;
return -1;
}
int cjIterations=0;
number_t cumTime=0;
bool ok=true;
ok = _algorithm->init(online);
if (! ok) {
cerr << __PRETTY_FUNCTION__ << " Error while initializing" << endl;
return -1;
}
_batchStatistics.clear();
if (_computeBatchStatistics)
_batchStatistics.resize(iterations);
OptimizationAlgorithm::SolverResult result = OptimizationAlgorithm::OK;
//循环开始每一轮优化
for (int i=0; i<iterations && ! terminate() && ok; i++){
preIteration(i);
if (_computeBatchStatistics) {
G2OBatchStatistics& cstat = _batchStatistics[i];
G2OBatchStatistics::setGlobalStats(&cstat);
cstat.iteration = i;
cstat.numEdges = _activeEdges.size();
cstat.numVertices = _activeVertices.size();
}
number_t ts = get_monotonic_time();
//调用求解器,求解此轮Δx的值
result = _algorithm->solve(i, online);
ok = ( result == OptimizationAlgorithm::OK );
bool errorComputed = false;
if (_computeBatchStatistics) {
computeActiveErrors();
errorComputed = true;
_batchStatistics[i].chi2 = activeRobustChi2();
_batchStatistics[i].timeIteration = get_monotonic_time()-ts;
}
if (verbose()){
number_t dts = get_monotonic_time()-ts;
cumTime += dts;
if (! errorComputed)
computeActiveErrors();
cerr << "iteration= " << i
<< "\t chi2= " << FIXED(activeRobustChi2())
<< "\t time= " << dts
<< "\t cumTime= " << cumTime
<< "\t edges= " << _activeEdges.size();
_algorithm->printVerbose(cerr);
cerr << endl;
}
++cjIterations;
postIteration(i);
}
if (result == OptimizationAlgorithm::Fail) {
return 0;
}
return cjIterations;
}
求解器求解此轮的Δx:
OptimizationAlgorithm::SolverResult OptimizationAlgorithmGaussNewton::solve(int iteration, bool online)
{
assert(_solver.optimizer() == _optimizer && "underlying linear solver operates on different graph");
bool ok = true;
//here so that correct component for max-mixtures can be computed before the build structure
number_t t=get_monotonic_time();
//调用优化器计算每个边的错误,会调用边提供的函数computeError
_optimizer->computeActiveErrors();
G2OBatchStatistics* globalStats = G2OBatchStatistics::globalStats();
if (globalStats) {
globalStats->timeResiduals = get_monotonic_time()-t;
}
if (iteration == 0 && !online) { // built up the CCS structure, here due to easy time measure
//构建黑森矩阵_Hpp(HessianPositionToPosistion),主要是方法里面的v->mapHessianMemory(m->data())把当前求解器里面的_Hpp的局部block映射到顶点里面的Hessian矩阵。
//这样在后续方法OptimizationAlgorithmGaussNewton::solve()
//-> BlockSolver<g2o::BlockSolverTraits<3, 1> >::buildSystem()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticForm()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormNs<0ul>()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormN<0>()
//中的代码from->A().noalias() += AtO * A;就可以通过更新顶点里的Hessian矩阵(A),间接达到更新_Hpp的目的。
ok = _solver.buildStructure();
if (! ok) {
cerr << __PRETTY_FUNCTION__ << ": Failure while building CCS structure" << endl;
return OptimizationAlgorithm::Fail;
}
}
t=get_monotonic_time();
//更新雅可比矩阵和目标向量b
_solver.buildSystem();
if (globalStats) {
globalStats->timeQuadraticForm = get_monotonic_time()-t;
t=get_monotonic_time();
}
//求解Δx
ok = _solver.solve();
if (globalStats) {
globalStats->timeLinearSolution = get_monotonic_time()-t;
t=get_monotonic_time();
}
//更新x = x + Δx
_optimizer->update(_solver.x());
if (globalStats) {
globalStats->timeUpdate = get_monotonic_time()-t;
}
if (ok)
return OK;
else
return Fail;
} |
OptimizationAlgorithm::SolverResult OptimizationAlgorithmGaussNewton::solve(int iteration, bool online)
{
assert(_solver.optimizer() == _optimizer && "underlying linear solver operates on different graph");
bool ok = true;
//here so that correct component for max-mixtures can be computed before the build structure
number_t t=get_monotonic_time();
//调用优化器计算每个边的错误,会调用边提供的函数computeError
_optimizer->computeActiveErrors();
G2OBatchStatistics* globalStats = G2OBatchStatistics::globalStats();
if (globalStats) {
globalStats->timeResiduals = get_monotonic_time()-t;
}
if (iteration == 0 && !online) { // built up the CCS structure, here due to easy time measure
//构建黑森矩阵_Hpp(HessianPositionToPosistion),主要是方法里面的v->mapHessianMemory(m->data())把当前求解器里面的_Hpp的局部block映射到顶点里面的Hessian矩阵。
//这样在后续方法OptimizationAlgorithmGaussNewton::solve()
//-> BlockSolver<g2o::BlockSolverTraits<3, 1> >::buildSystem()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticForm()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormNs<0ul>()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormN<0>()
//中的代码from->A().noalias() += AtO * A;就可以通过更新顶点里的Hessian矩阵(A),间接达到更新_Hpp的目的。
ok = _solver.buildStructure();
if (! ok) {
cerr << __PRETTY_FUNCTION__ << ": Failure while building CCS structure" << endl;
return OptimizationAlgorithm::Fail;
}
}
t=get_monotonic_time();
//更新雅可比矩阵和目标向量b
_solver.buildSystem();
if (globalStats) {
globalStats->timeQuadraticForm = get_monotonic_time()-t;
t=get_monotonic_time();
}
//求解Δx
ok = _solver.solve();
if (globalStats) {
globalStats->timeLinearSolution = get_monotonic_time()-t;
t=get_monotonic_time();
}
//更新x = x + Δx
_optimizer->update(_solver.x());
if (globalStats) {
globalStats->timeUpdate = get_monotonic_time()-t;
}
if (ok)
return OK;
else
return Fail;
}
更新雅可比矩阵和目标向量b
template <typename Traits>
bool BlockSolver<Traits>::buildSystem()
{
// clear b vector
# ifdef G2O_OPENMP
# pragma omp parallel for default (shared) if (_optimizer->indexMapping().size() > 1000)
# endif
for (int i = 0; i < static_cast<int>(_optimizer->indexMapping().size()); ++i) {
OptimizableGraph::Vertex* v=_optimizer->indexMapping()[i];
assert(v);
v->clearQuadraticForm();
}
_Hpp->clear();
if (_doSchur) {
_Hll->clear();
_Hpl->clear();
}
// resetting the terms for the pairwise constraints
// built up the current system by storing the Hessian blocks in the edges and vertices
# ifndef G2O_OPENMP
// no threading, we do not need to copy the workspace
JacobianWorkspace& jacobianWorkspace = _optimizer->jacobianWorkspace();
# else
// if running with threads need to produce copies of the workspace for each thread
JacobianWorkspace jacobianWorkspace = _optimizer->jacobianWorkspace();
# pragma omp parallel for default (shared) firstprivate(jacobianWorkspace) if (_optimizer->activeEdges().size() > 100)
# endif
for (int k = 0; k < static_cast<int>(_optimizer->activeEdges().size()); ++k) {
OptimizableGraph::Edge* e = _optimizer->activeEdges()[k];
//对每个边(误差函数)进行计算,完成雅可比矩阵J的更新,这儿会调用CurveFittingEdge::linearizeOplus
e->linearizeOplus(jacobianWorkspace); // jacobian of the nodes' oplus (manifold)
//对边里面的顶点的hessian矩阵(A)和b进行更新
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticForm()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormNs<0ul>()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormN<0>()
// 更新b值 b += JT * fx: from->b().noalias() += A.transpose() * weightedError;
// 更新hessian矩阵H += JT * J:from->A().noalias() += AtO * A;
//因为前面的v->mapHessianMemory(m->data()),所有_Hpp同时更新了,因为是同一个内存地址。
e->constructQuadraticForm();
# ifndef NDEBUG
for (size_t i = 0; i < e->vertices().size(); ++i) {
const OptimizableGraph::Vertex* v = static_cast<const OptimizableGraph::Vertex*>(e->vertex(i));
if (! v->fixed()) {
bool hasANan = arrayHasNaN(jacobianWorkspace.workspaceForVertex(i), e->dimension() * v->dimension());
if (hasANan) {
std::cerr << "buildSystem(): NaN within Jacobian for edge " << e << " for vertex " << i << std::endl;
break;
}
}
}
# endif
}
// flush the current system in a sparse block matrix
# ifdef G2O_OPENMP
# pragma omp parallel for default (shared) if (_optimizer->indexMapping().size() > 1000)
# endif
for (int i = 0; i < static_cast<int>(_optimizer->indexMapping().size()); ++i) {
OptimizableGraph::Vertex* v=_optimizer->indexMapping()[i];
int iBase = v->colInHessian();
if (v->marginalized())
iBase+=_sizePoses;
//把顶点中的b更新到_b中,到此优化器中的_Hpp和_b都完成了更新
v->copyB(_b+iBase);
}
return false;
} |
template <typename Traits>
bool BlockSolver<Traits>::buildSystem()
{
// clear b vector
# ifdef G2O_OPENMP
# pragma omp parallel for default (shared) if (_optimizer->indexMapping().size() > 1000)
# endif
for (int i = 0; i < static_cast<int>(_optimizer->indexMapping().size()); ++i) {
OptimizableGraph::Vertex* v=_optimizer->indexMapping()[i];
assert(v);
v->clearQuadraticForm();
}
_Hpp->clear();
if (_doSchur) {
_Hll->clear();
_Hpl->clear();
}
// resetting the terms for the pairwise constraints
// built up the current system by storing the Hessian blocks in the edges and vertices
# ifndef G2O_OPENMP
// no threading, we do not need to copy the workspace
JacobianWorkspace& jacobianWorkspace = _optimizer->jacobianWorkspace();
# else
// if running with threads need to produce copies of the workspace for each thread
JacobianWorkspace jacobianWorkspace = _optimizer->jacobianWorkspace();
# pragma omp parallel for default (shared) firstprivate(jacobianWorkspace) if (_optimizer->activeEdges().size() > 100)
# endif
for (int k = 0; k < static_cast<int>(_optimizer->activeEdges().size()); ++k) {
OptimizableGraph::Edge* e = _optimizer->activeEdges()[k];
//对每个边(误差函数)进行计算,完成雅可比矩阵J的更新,这儿会调用CurveFittingEdge::linearizeOplus
e->linearizeOplus(jacobianWorkspace); // jacobian of the nodes' oplus (manifold)
//对边里面的顶点的hessian矩阵(A)和b进行更新
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticForm()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormNs<0ul>()
//-> BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormN<0>()
// 更新b值 b += JT * fx: from->b().noalias() += A.transpose() * weightedError;
// 更新hessian矩阵H += JT * J:from->A().noalias() += AtO * A;
//因为前面的v->mapHessianMemory(m->data()),所有_Hpp同时更新了,因为是同一个内存地址。
e->constructQuadraticForm();
# ifndef NDEBUG
for (size_t i = 0; i < e->vertices().size(); ++i) {
const OptimizableGraph::Vertex* v = static_cast<const OptimizableGraph::Vertex*>(e->vertex(i));
if (! v->fixed()) {
bool hasANan = arrayHasNaN(jacobianWorkspace.workspaceForVertex(i), e->dimension() * v->dimension());
if (hasANan) {
std::cerr << "buildSystem(): NaN within Jacobian for edge " << e << " for vertex " << i << std::endl;
break;
}
}
}
# endif
}
// flush the current system in a sparse block matrix
# ifdef G2O_OPENMP
# pragma omp parallel for default (shared) if (_optimizer->indexMapping().size() > 1000)
# endif
for (int i = 0; i < static_cast<int>(_optimizer->indexMapping().size()); ++i) {
OptimizableGraph::Vertex* v=_optimizer->indexMapping()[i];
int iBase = v->colInHessian();
if (v->marginalized())
iBase+=_sizePoses;
//把顶点中的b更新到_b中,到此优化器中的_Hpp和_b都完成了更新
v->copyB(_b+iBase);
}
return false;
}
计算雅可比矩阵
//模板展开g2o::BaseFixedSizedEdge<1, Eigen::Matrix<double, 2, 1, 0, 2, 1>, VertexCircle>::linearizeOplus() at base_fixed_sized_edge.hpp:130
template <int D, typename E, typename... VertexTypes>
void BaseFixedSizedEdge<D, E, VertexTypes...>::linearizeOplus(
JacobianWorkspace& jacobianWorkspace) {
linearizeOplus_allocate(jacobianWorkspace, std::make_index_sequence<_nr_of_vertices>());
//误差函数(边)需要提供此方法,不管是手动计算还是采用自动微分计算
linearizeOplus();
}
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
// 计算曲线模型误差
virtual void computeError() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
//误差 = 测量值 - 预测值
_error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
}
// 计算雅可比矩阵,这儿是手动计算雅可比矩阵
virtual void linearizeOplus() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
//y的计算值
double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
//雅可比矩阵1x3 参数向量3x1 y值1x1
//对第一个参数abc[0]的导数
_jacobianOplusXi[0] = -_x * _x * y;
//对第二个参数abc[1]的导数
_jacobianOplusXi[1] = -_x * y;
//对第三个参数abc[2]的导数
_jacobianOplusXi[2] = -y;
} |
//模板展开g2o::BaseFixedSizedEdge<1, Eigen::Matrix<double, 2, 1, 0, 2, 1>, VertexCircle>::linearizeOplus() at base_fixed_sized_edge.hpp:130
template <int D, typename E, typename... VertexTypes>
void BaseFixedSizedEdge<D, E, VertexTypes...>::linearizeOplus(
JacobianWorkspace& jacobianWorkspace) {
linearizeOplus_allocate(jacobianWorkspace, std::make_index_sequence<_nr_of_vertices>());
//误差函数(边)需要提供此方法,不管是手动计算还是采用自动微分计算
linearizeOplus();
}
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
// 计算曲线模型误差
virtual void computeError() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
//误差 = 测量值 - 预测值
_error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
}
// 计算雅可比矩阵,这儿是手动计算雅可比矩阵
virtual void linearizeOplus() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
//y的计算值
double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
//雅可比矩阵1x3 参数向量3x1 y值1x1
//对第一个参数abc[0]的导数
_jacobianOplusXi[0] = -_x * _x * y;
//对第二个参数abc[1]的导数
_jacobianOplusXi[1] = -_x * y;
//对第三个参数abc[2]的导数
_jacobianOplusXi[2] = -y;
}
更新雅可比矩阵
//构建参数的二次形式
template <int D, typename E, typename... VertexTypes>
void BaseFixedSizedEdge<D, E, VertexTypes...>::constructQuadraticForm() {
if (this->robustKernel()) {
number_t error = this->chi2();
Vector3 rho;
this->robustKernel()->robustify(error, rho);
Eigen::Matrix<number_t, D, 1, Eigen::ColMajor> omega_r = -_information * _error;
omega_r *= rho[1];
constructQuadraticFormNs(this->robustInformation(rho), omega_r,
std::make_index_sequence<_nr_of_vertices>());
} else {
constructQuadraticFormNs(_information, -_information * _error,
std::make_index_sequence<_nr_of_vertices>());
}
}
//模板展开后为g2o::BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormNs<0ul>() at base_fixed_sized_edge.hpp:66
template <int D, typename E, typename... VertexTypes>
template <std::size_t... Ints>
void BaseFixedSizedEdge<D, E, VertexTypes...>::constructQuadraticFormNs(
const InformationType& omega, const ErrorVector& weightedError, std::index_sequence<Ints...>) {
int unused[] = {(constructQuadraticFormN<Ints>(omega, weightedError), 0)...};
(void)unused;
}
template <int D, typename E, typename... VertexTypes>
template <int N>
void BaseFixedSizedEdge<D, E, VertexTypes...>::constructQuadraticFormN(
const InformationType& omega, const ErrorVector& weightedError) {
//获取当前边的点(参数),然后更新雅可比矩阵A和偏差b,用于后边求x(Ax=b)
auto from = vertexXn<N>();
//获取雅可比矩阵
const auto& A = std::get<N>(_jacobianOplus);
if (!(from->fixed())) {
const auto AtO = A.transpose() * omega;
{
internal::QuadraticFormLock lck(*from);
(void)lck;
//根据上篇文章的公式,b=AT * error,error为实际值和预测值的差。
from->b().noalias() += A.transpose() * weightedError;
//H = AT * A,累计Hessian矩阵
from->A().noalias() += AtO * A;
}
constructOffDiagonalQuadraticFormMs<N>(AtO, std::make_index_sequence<_nr_of_vertices - N - 1>());
}
}; |
//构建参数的二次形式
template <int D, typename E, typename... VertexTypes>
void BaseFixedSizedEdge<D, E, VertexTypes...>::constructQuadraticForm() {
if (this->robustKernel()) {
number_t error = this->chi2();
Vector3 rho;
this->robustKernel()->robustify(error, rho);
Eigen::Matrix<number_t, D, 1, Eigen::ColMajor> omega_r = -_information * _error;
omega_r *= rho[1];
constructQuadraticFormNs(this->robustInformation(rho), omega_r,
std::make_index_sequence<_nr_of_vertices>());
} else {
constructQuadraticFormNs(_information, -_information * _error,
std::make_index_sequence<_nr_of_vertices>());
}
}
//模板展开后为g2o::BaseFixedSizedEdge<1, double, CurveFittingVertex>::constructQuadraticFormNs<0ul>() at base_fixed_sized_edge.hpp:66
template <int D, typename E, typename... VertexTypes>
template <std::size_t... Ints>
void BaseFixedSizedEdge<D, E, VertexTypes...>::constructQuadraticFormNs(
const InformationType& omega, const ErrorVector& weightedError, std::index_sequence<Ints...>) {
int unused[] = {(constructQuadraticFormN<Ints>(omega, weightedError), 0)...};
(void)unused;
}
template <int D, typename E, typename... VertexTypes>
template <int N>
void BaseFixedSizedEdge<D, E, VertexTypes...>::constructQuadraticFormN(
const InformationType& omega, const ErrorVector& weightedError) {
//获取当前边的点(参数),然后更新雅可比矩阵A和偏差b,用于后边求x(Ax=b)
auto from = vertexXn<N>();
//获取雅可比矩阵
const auto& A = std::get<N>(_jacobianOplus);
if (!(from->fixed())) {
const auto AtO = A.transpose() * omega;
{
internal::QuadraticFormLock lck(*from);
(void)lck;
//根据上篇文章的公式,b=AT * error,error为实际值和预测值的差。
from->b().noalias() += A.transpose() * weightedError;
//H = AT * A,累计Hessian矩阵
from->A().noalias() += AtO * A;
}
constructOffDiagonalQuadraticFormMs<N>(AtO, std::make_index_sequence<_nr_of_vertices - N - 1>());
}
};
求解 _Hpp * _x = _b 得到 _x
template <typename Traits>
bool BlockSolver<Traits>::solve(){
//cerr << __PRETTY_FUNCTION__ << endl;
if (! _doSchur){
number_t t=get_monotonic_time();
//利用稀疏矩阵的分解,求解_x
bool ok = _linearSolver->solve(*_Hpp, _x, _b);
G2OBatchStatistics* globalStats = G2OBatchStatistics::globalStats();
if (globalStats) {
globalStats->timeLinearSolver = get_monotonic_time() - t;
globalStats->hessianDimension = globalStats->hessianPoseDimension = _Hpp->cols();
}
return ok;
}
// schur thing
// backup the coefficient matrix
number_t t=get_monotonic_time();
// _Hschur = _Hpp, but keeping the pattern of _Hschur
_Hschur->clear();
_Hpp->add(*_Hschur);
//_DInvSchur->clear();
memset(_coefficients.get(), 0, _sizePoses*sizeof(number_t));
# ifdef G2O_OPENMP
# pragma omp parallel for default (shared) schedule(dynamic, 10)
# endif
for (int landmarkIndex = 0; landmarkIndex < static_cast<int>(_Hll->blockCols().size()); ++landmarkIndex) {
const typename SparseBlockMatrix<LandmarkMatrixType>::IntBlockMap& marginalizeColumn = _Hll->blockCols()[landmarkIndex];
assert(marginalizeColumn.size() == 1 && "more than one block in _Hll column");
// calculate inverse block for the landmark
const LandmarkMatrixType * D = marginalizeColumn.begin()->second;
assert (D && D->rows()==D->cols() && "Error in landmark matrix");
LandmarkMatrixType& Dinv = _DInvSchur->diagonal()[landmarkIndex];
Dinv = D->inverse();
LandmarkVectorType db(D->rows());
for (int j=0; j<D->rows(); ++j) {
db[j]=_b[_Hll->rowBaseOfBlock(landmarkIndex) + _sizePoses + j];
}
db=Dinv*db;
assert((size_t)landmarkIndex < _HplCCS->blockCols().size() && "Index out of bounds");
const typename SparseBlockMatrixCCS<PoseLandmarkMatrixType>::SparseColumn& landmarkColumn = _HplCCS->blockCols()[landmarkIndex];
for (typename SparseBlockMatrixCCS<PoseLandmarkMatrixType>::SparseColumn::const_iterator it_outer = landmarkColumn.begin();
it_outer != landmarkColumn.end(); ++it_outer) {
int i1 = it_outer->row;
const PoseLandmarkMatrixType* Bi = it_outer->block;
assert(Bi);
PoseLandmarkMatrixType BDinv = (*Bi)*(Dinv);
assert(_HplCCS->rowBaseOfBlock(i1) < _sizePoses && "Index out of bounds");
typename PoseVectorType::MapType Bb(&_coefficients[_HplCCS->rowBaseOfBlock(i1)], Bi->rows());
# ifdef G2O_OPENMP
ScopedOpenMPMutex mutexLock(&_coefficientsMutex[i1]);
# endif
Bb.noalias() += (*Bi)*db;
assert(i1 >= 0 && i1 < static_cast<int>(_HschurTransposedCCS->blockCols().size()) && "Index out of bounds");
typename SparseBlockMatrixCCS<PoseMatrixType>::SparseColumn::iterator targetColumnIt = _HschurTransposedCCS->blockCols()[i1].begin();
typename SparseBlockMatrixCCS<PoseLandmarkMatrixType>::RowBlock aux(i1, 0);
typename SparseBlockMatrixCCS<PoseLandmarkMatrixType>::SparseColumn::const_iterator it_inner = lower_bound(landmarkColumn.begin(), landmarkColumn.end(), aux);
for (; it_inner != landmarkColumn.end(); ++it_inner) {
int i2 = it_inner->row;
const PoseLandmarkMatrixType* Bj = it_inner->block;
assert(Bj);
while (targetColumnIt->row < i2 /*&& targetColumnIt != _HschurTransposedCCS->blockCols()[i1].end()*/)
++targetColumnIt;
assert(targetColumnIt != _HschurTransposedCCS->blockCols()[i1].end() && targetColumnIt->row == i2 && "invalid iterator, something wrong with the matrix structure");
PoseMatrixType* Hi1i2 = targetColumnIt->block;//_Hschur->block(i1,i2);
assert(Hi1i2);
(*Hi1i2).noalias() -= BDinv*Bj->transpose();
}
}
}
//cerr << "Solve [marginalize] = " << get_monotonic_time()-t << endl;
// _bschur = _b for calling solver, and not touching _b
memcpy(_bschur.get(), _b, _sizePoses * sizeof(number_t));
for (int i=0; i<_sizePoses; ++i){
_bschur[i]-=_coefficients[i];
}
G2OBatchStatistics* globalStats = G2OBatchStatistics::globalStats();
if (globalStats){
globalStats->timeSchurComplement = get_monotonic_time() - t;
}
t=get_monotonic_time();
bool solvedPoses = _linearSolver->solve(*_Hschur, _x, _bschur.get());
if (globalStats) {
globalStats->timeLinearSolver = get_monotonic_time() - t;
globalStats->hessianPoseDimension = _Hpp->cols();
globalStats->hessianLandmarkDimension = _Hll->cols();
globalStats->hessianDimension = globalStats->hessianPoseDimension + globalStats->hessianLandmarkDimension;
}
//cerr << "Solve [decompose and solve] = " << get_monotonic_time()-t << endl;
if (! solvedPoses)
return false;
// _x contains the solution for the poses, now applying it to the landmarks to get the new part of the
// solution;
number_t* xp = _x;
number_t* cp = _coefficients.get();
number_t* xl=_x+_sizePoses;
number_t* cl=_coefficients.get() + _sizePoses;
number_t* bl=_b+_sizePoses;
// cp = -xp
for (int i=0; i<_sizePoses; ++i)
cp[i]=-xp[i];
// cl = bl
memcpy(cl,bl,_sizeLandmarks*sizeof(number_t));
// cl = bl - Bt * xp
//Bt->multiply(cl, cp);
_HplCCS->rightMultiply(cl, cp);
// xl = Dinv * cl
memset(xl,0, _sizeLandmarks*sizeof(number_t));
_DInvSchur->multiply(xl,cl);
//_DInvSchur->rightMultiply(xl,cl);
//cerr << "Solve [landmark delta] = " << get_monotonic_time()-t << endl;
return true;
} |
template <typename Traits>
bool BlockSolver<Traits>::solve(){
//cerr << __PRETTY_FUNCTION__ << endl;
if (! _doSchur){
number_t t=get_monotonic_time();
//利用稀疏矩阵的分解,求解_x
bool ok = _linearSolver->solve(*_Hpp, _x, _b);
G2OBatchStatistics* globalStats = G2OBatchStatistics::globalStats();
if (globalStats) {
globalStats->timeLinearSolver = get_monotonic_time() - t;
globalStats->hessianDimension = globalStats->hessianPoseDimension = _Hpp->cols();
}
return ok;
}
// schur thing
// backup the coefficient matrix
number_t t=get_monotonic_time();
// _Hschur = _Hpp, but keeping the pattern of _Hschur
_Hschur->clear();
_Hpp->add(*_Hschur);
//_DInvSchur->clear();
memset(_coefficients.get(), 0, _sizePoses*sizeof(number_t));
# ifdef G2O_OPENMP
# pragma omp parallel for default (shared) schedule(dynamic, 10)
# endif
for (int landmarkIndex = 0; landmarkIndex < static_cast<int>(_Hll->blockCols().size()); ++landmarkIndex) {
const typename SparseBlockMatrix<LandmarkMatrixType>::IntBlockMap& marginalizeColumn = _Hll->blockCols()[landmarkIndex];
assert(marginalizeColumn.size() == 1 && "more than one block in _Hll column");
// calculate inverse block for the landmark
const LandmarkMatrixType * D = marginalizeColumn.begin()->second;
assert (D && D->rows()==D->cols() && "Error in landmark matrix");
LandmarkMatrixType& Dinv = _DInvSchur->diagonal()[landmarkIndex];
Dinv = D->inverse();
LandmarkVectorType db(D->rows());
for (int j=0; j<D->rows(); ++j) {
db[j]=_b[_Hll->rowBaseOfBlock(landmarkIndex) + _sizePoses + j];
}
db=Dinv*db;
assert((size_t)landmarkIndex < _HplCCS->blockCols().size() && "Index out of bounds");
const typename SparseBlockMatrixCCS<PoseLandmarkMatrixType>::SparseColumn& landmarkColumn = _HplCCS->blockCols()[landmarkIndex];
for (typename SparseBlockMatrixCCS<PoseLandmarkMatrixType>::SparseColumn::const_iterator it_outer = landmarkColumn.begin();
it_outer != landmarkColumn.end(); ++it_outer) {
int i1 = it_outer->row;
const PoseLandmarkMatrixType* Bi = it_outer->block;
assert(Bi);
PoseLandmarkMatrixType BDinv = (*Bi)*(Dinv);
assert(_HplCCS->rowBaseOfBlock(i1) < _sizePoses && "Index out of bounds");
typename PoseVectorType::MapType Bb(&_coefficients[_HplCCS->rowBaseOfBlock(i1)], Bi->rows());
# ifdef G2O_OPENMP
ScopedOpenMPMutex mutexLock(&_coefficientsMutex[i1]);
# endif
Bb.noalias() += (*Bi)*db;
assert(i1 >= 0 && i1 < static_cast<int>(_HschurTransposedCCS->blockCols().size()) && "Index out of bounds");
typename SparseBlockMatrixCCS<PoseMatrixType>::SparseColumn::iterator targetColumnIt = _HschurTransposedCCS->blockCols()[i1].begin();
typename SparseBlockMatrixCCS<PoseLandmarkMatrixType>::RowBlock aux(i1, 0);
typename SparseBlockMatrixCCS<PoseLandmarkMatrixType>::SparseColumn::const_iterator it_inner = lower_bound(landmarkColumn.begin(), landmarkColumn.end(), aux);
for (; it_inner != landmarkColumn.end(); ++it_inner) {
int i2 = it_inner->row;
const PoseLandmarkMatrixType* Bj = it_inner->block;
assert(Bj);
while (targetColumnIt->row < i2 /*&& targetColumnIt != _HschurTransposedCCS->blockCols()[i1].end()*/)
++targetColumnIt;
assert(targetColumnIt != _HschurTransposedCCS->blockCols()[i1].end() && targetColumnIt->row == i2 && "invalid iterator, something wrong with the matrix structure");
PoseMatrixType* Hi1i2 = targetColumnIt->block;//_Hschur->block(i1,i2);
assert(Hi1i2);
(*Hi1i2).noalias() -= BDinv*Bj->transpose();
}
}
}
//cerr << "Solve [marginalize] = " << get_monotonic_time()-t << endl;
// _bschur = _b for calling solver, and not touching _b
memcpy(_bschur.get(), _b, _sizePoses * sizeof(number_t));
for (int i=0; i<_sizePoses; ++i){
_bschur[i]-=_coefficients[i];
}
G2OBatchStatistics* globalStats = G2OBatchStatistics::globalStats();
if (globalStats){
globalStats->timeSchurComplement = get_monotonic_time() - t;
}
t=get_monotonic_time();
bool solvedPoses = _linearSolver->solve(*_Hschur, _x, _bschur.get());
if (globalStats) {
globalStats->timeLinearSolver = get_monotonic_time() - t;
globalStats->hessianPoseDimension = _Hpp->cols();
globalStats->hessianLandmarkDimension = _Hll->cols();
globalStats->hessianDimension = globalStats->hessianPoseDimension + globalStats->hessianLandmarkDimension;
}
//cerr << "Solve [decompose and solve] = " << get_monotonic_time()-t << endl;
if (! solvedPoses)
return false;
// _x contains the solution for the poses, now applying it to the landmarks to get the new part of the
// solution;
number_t* xp = _x;
number_t* cp = _coefficients.get();
number_t* xl=_x+_sizePoses;
number_t* cl=_coefficients.get() + _sizePoses;
number_t* bl=_b+_sizePoses;
// cp = -xp
for (int i=0; i<_sizePoses; ++i)
cp[i]=-xp[i];
// cl = bl
memcpy(cl,bl,_sizeLandmarks*sizeof(number_t));
// cl = bl - Bt * xp
//Bt->multiply(cl, cp);
_HplCCS->rightMultiply(cl, cp);
// xl = Dinv * cl
memset(xl,0, _sizeLandmarks*sizeof(number_t));
_DInvSchur->multiply(xl,cl);
//_DInvSchur->rightMultiply(xl,cl);
//cerr << "Solve [landmark delta] = " << get_monotonic_time()-t << endl;
return true;
}
通过Δx更新x
void SparseOptimizer::update(const number_t* update)
{
// update the graph by calling oplus on the vertices
for (size_t i=0; i < _ivMap.size(); ++i) {
OptimizableGraph::Vertex* v= _ivMap[i];
#ifndef NDEBUG
bool hasNan = arrayHasNaN(update, v->dimension());
if (hasNan)
cerr << __PRETTY_FUNCTION__ << ": Update contains a nan for vertex " << v->id() << endl;
#endif
//这儿会调用CurveFittingVertex::oplusImpl完成顶点参数更新
v->oplus(update);
update += v->dimension();
}
} |
void SparseOptimizer::update(const number_t* update)
{
// update the graph by calling oplus on the vertices
for (size_t i=0; i < _ivMap.size(); ++i) {
OptimizableGraph::Vertex* v= _ivMap[i];
#ifndef NDEBUG
bool hasNan = arrayHasNaN(update, v->dimension());
if (hasNan)
cerr << __PRETTY_FUNCTION__ << ": Update contains a nan for vertex " << v->id() << endl;
#endif
//这儿会调用CurveFittingVertex::oplusImpl完成顶点参数更新
v->oplus(update);
update += v->dimension();
}
}
本作品采用知识共享署名 4.0 国际许可协议进行许可。
