BFGS方法推导
可以构造一个二次函数来开始,假设![]() 第k次迭代为:
第k次迭代为:
![]()
注意![]() 为n x n对称正定矩阵,可以在每次迭代中更新。注意到这个构造函数在p=0的时候,
为n x n对称正定矩阵,可以在每次迭代中更新。注意到这个构造函数在p=0的时候,![]() 和
和![]() 和原函数是相同的。对其求导,得到
和原函数是相同的。对其求导,得到
![]()
公式2即为搜索方向向量,由此![]() 第k+1次迭代为(其中
第k+1次迭代为(其中![]() 可以用强Wolfe准则来计算):
可以用强Wolfe准则来计算):
![]()
为了不每次都计算![]() (计算太复杂),Davidon提出用最近迭代的几步来计算它。
(计算太复杂),Davidon提出用最近迭代的几步来计算它。
我们已经计算出![]() ,现在构造其在k+1次迭代的二次函数:
,现在构造其在k+1次迭代的二次函数:
![]()
怎么求![]() 呢?函数
呢?函数![]() 应该在
应该在![]() 处和
处和![]() 处和目标函数
处和目标函数![]() 导数一致。对其求导,并令
导数一致。对其求导,并令![]() ,即
,即![]() 处得:(
处得:(![]() 处自然相等,
处自然相等,![]() )
)
![]()
调整方程得:
![]()
令![]() ,方程6为:
,方程6为:
![]()
令![]() ,得到另一个形式:
,得到另一个形式:
![]()
由此,方程2可以写为:
![]()
由于我们需要一个比较简单的更新![]() 的方法,令:
的方法,令:
![]()
其中![]() 和
和![]() 为秩1或秩2的矩阵。
为秩1或秩2的矩阵。
令![]() 为:
为:
![]()
联立方程7,方程10和方程11得:
![]()
等价于:
![]()
通过方程13发现,![]() 和
和![]() 不唯一,令
不唯一,令![]() 和
和![]() 分别平行于
分别平行于![]() 和
和![]() ,即
,即![]() 和
和![]() ,带入方程11得:
,带入方程11得:
![]()
把![]() 和
和![]() 带入方程13得:
带入方程13得:
![]()
整理后得到:
![]()
所以![]() ,
,![]() ,
,
即![]() ,
,![]() 。
。
最后联立方程14,代入到方程10得:
![]()
用同样的方式可以得到:
![]()
Sherman Morison Woodbury公式:
![]()
下面对方程18应用Sherman Morison Woodbury公式:(注意推导中的![]() 是方程中的
是方程中的![]() )(参考文档):
)(参考文档):

现在我们得到结果:
![]()
令![]() ,方程19可得BFGS方法的迭代方程:
,方程19可得BFGS方法的迭代方程:
![]()
LBFGS方法推导
令![]() ,则BFGS方程可写成:
,则BFGS方程可写成:
![]()
参考文档
则从k=0开始有:
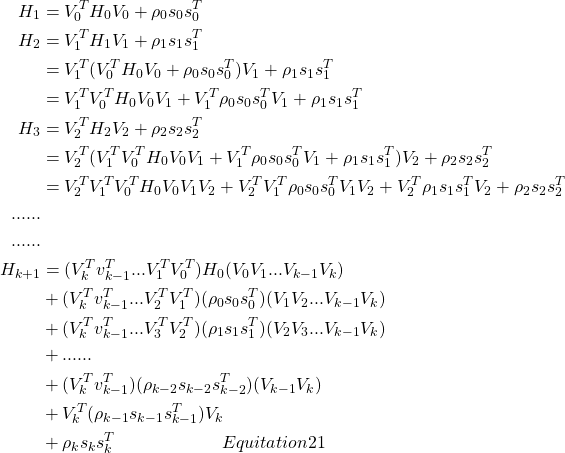
由上面可见,计算![]() 需要用到
需要用到![]() 组数据,数据量非常大,LBFGS算法就采取只去最近的m组数据来运算,即可以构造近似计算公式:
组数据,数据量非常大,LBFGS算法就采取只去最近的m组数据来运算,即可以构造近似计算公式:
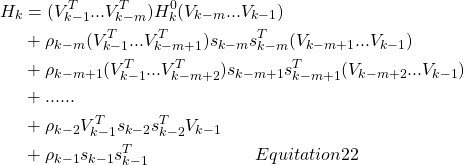
最后Numerial Optimization 这本书给出了LBFGS的双向循环算法:
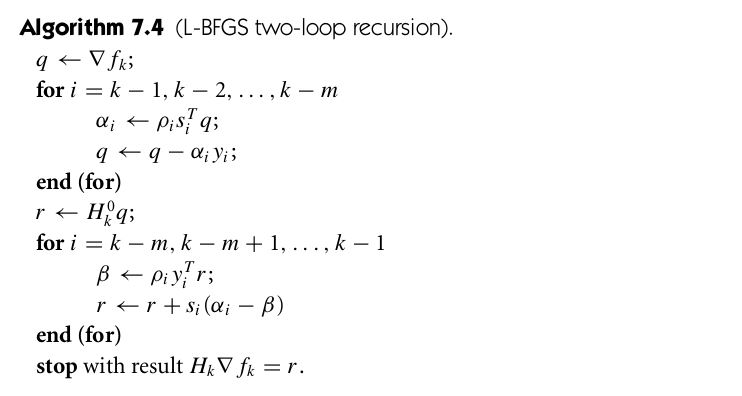
具体实现代码可以参见Breeze LBFGS
最后验证算法对公式22的正确性:参考文档
令![]() :
:
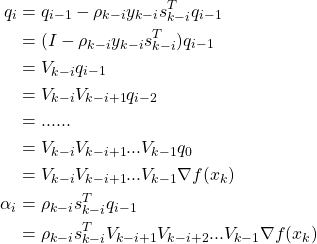
令![]() ,这里的m指的是从现在到历史记录m次的后一次,因为LBFGS只记录m次历史:
,这里的m指的是从现在到历史记录m次的后一次,因为LBFGS只记录m次历史:
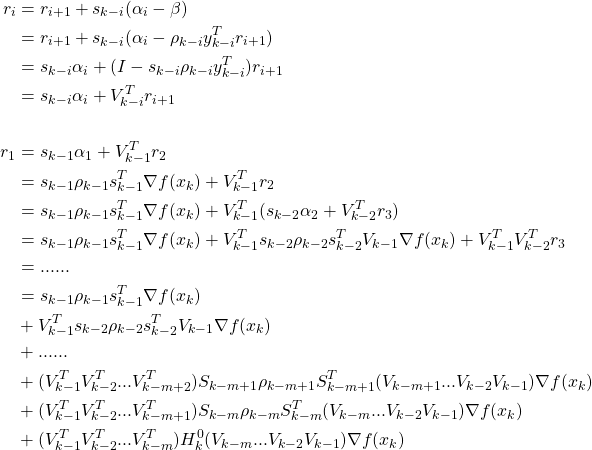
本作品采用知识共享署名 4.0 国际许可协议进行许可。