Logistic Regression(逻辑回归) in ML

class LogisticRegressionSuite
  extends SparkFunSuite with MLlibTestSparkContext with DefaultReadWriteTest {
 
  import testImplicits._ //Mark A
 
  private val seed = 42
  @transient var smallBinaryDataset: Dataset[_] = _  //Mark B
 
  override def beforeAll(): Unit = {
    super.beforeAll()
 
    smallBinaryDataset = generateLogisticInput(1.0, 1.0, nPoints = 100, seed = seed).toDF()  //Mark C
 
......
 
  test("logistic regression: default params") {
    val lr = new LogisticRegression
    assert(lr.getLabelCol === "label")
    assert(lr.getFeaturesCol === "features")
    assert(lr.getPredictionCol === "prediction")
    assert(lr.getRawPredictionCol === "rawPrediction")
    assert(lr.getProbabilityCol === "probability")
    assert(lr.getFamily === "auto")
    assert(!lr.isDefined(lr.weightCol))
    assert(lr.getFitIntercept)
    assert(lr.getStandardization)
    val model = lr.fit(smallBinaryDataset)
    model.transform(smallBinaryDataset)
      .select("label", "probability", "prediction", "rawPrediction")
      .collect()
    assert(model.getThreshold === 0.5)
    assert(model.getFeaturesCol === "features")
    assert(model.getPredictionCol === "prediction")
    assert(model.getRawPredictionCol === "rawPrediction")
    assert(model.getProbabilityCol === "probability")
    assert(model.intercept !== 0.0)
    assert(model.hasParent)
 
    // copied model must have the same parent.
    MLTestingUtils.checkCopy(model)
    assert(model.hasSummary)
    val copiedModel = model.copy(ParamMap.empty)
    assert(copiedModel.hasSummary)
    model.setSummary(None)
    assert(!model.hasSummary)
  }
 
......
 
object LogisticRegressionSuite {
 
......
 
  // Generate input of the form Y = logistic(offset + scale*X)
  def generateLogisticInput(
      offset: Double,
      scale: Double,
      nPoints: Int,
      seed: Int): Seq[LabeledPoint] = {
    val rnd = new Random(seed)
    val x1 = Array.fill[Double](nPoints)(rnd.nextGaussian())
 
    val y = (0 until nPoints).map { i =>
      val p = 1.0 / (1.0 + math.exp(-(offset + scale * x1(i))))
      if (rnd.nextDouble() < p) 1.0 else 0.0 } val testData = (0 until nPoints).map(i => LabeledPoint(y(i), Vectors.dense(Array(x1(i)))))
    testData
  }
......

abstract class SQLImplicits {
......
  /**
   * Creates a [[Dataset]] from a local Seq.
   * @since 1.6.0
   */
  implicit def localSeqToDatasetHolder[T : Encoder](s: Seq[T]): DatasetHolder[T] = {
    DatasetHolder(_sqlContext.createDataset(s))
  }
......
 
case class DatasetHolder[T] private[sql](private val ds: Dataset[T]) {
 
  // This is declared with parentheses to prevent the Scala compiler from treating
  // `rdd.toDS("1")` as invoking this toDS and then apply on the returned Dataset.
  def toDS(): Dataset[T] = ds
 
  // This is declared with parentheses to prevent the Scala compiler from treating
  // `rdd.toDF("1")` as invoking this toDF and then apply on the returned DataFrame.
  def toDF(): DataFrame = ds.toDF()
 
  def toDF(colNames: String*): DataFrame = ds.toDF(colNames : _*)
}

  override def fit(dataset: Dataset[_]): M = {
    // This handles a few items such as schema validation.
    // Developers only need to implement train().
    transformSchema(dataset.schema, logging = true)
 
    // Cast LabelCol to DoubleType and keep the metadata.
    val labelMeta = dataset.schema($(labelCol)).metadata
    val casted = dataset.withColumn($(labelCol), col($(labelCol)).cast(DoubleType), labelMeta)
 
    copyValues(train(casted).setParent(this))
  }
 
  override protected[spark] def train(dataset: Dataset[_]): LogisticRegressionModel = {
    val handlePersistence = dataset.rdd.getStorageLevel == StorageLevel.NONE
    train(dataset, handlePersistence)
  }
 
  protected[spark] def train(dataset: Dataset[_], handlePersistence: Boolean):
      LogisticRegressionModel = {
    val w = if (!isDefined(weightCol) || $(weightCol).isEmpty) lit(1.0) else col($(weightCol))
    val instances: RDD[Instance] =
      dataset.select(col($(labelCol)), w, col($(featuresCol))).rdd.map {
        case Row(label: Double, weight: Double, features: Vector) =>
          Instance(label, weight, features)
      }
 
    if (handlePersistence) instances.persist(StorageLevel.MEMORY_AND_DISK)
 
    val instr = Instrumentation.create(this, instances)
    instr.logParams(regParam, elasticNetParam, standardization, threshold,
      maxIter, tol, fitIntercept)

    val (summarizer, labelSummarizer) = {
      val seqOp = (c: (MultivariateOnlineSummarizer, MultiClassSummarizer),
        instance: Instance) =>
          (c._1.add(instance.features, instance.weight), c._2.add(instance.label, instance.weight))
 
      val combOp = (c1: (MultivariateOnlineSummarizer, MultiClassSummarizer),
        c2: (MultivariateOnlineSummarizer, MultiClassSummarizer)) =>
          (c1._1.merge(c2._1), c1._2.merge(c2._2))
 
      instances.treeAggregate(
        new MultivariateOnlineSummarizer, new MultiClassSummarizer
      )(seqOp, combOp, $(aggregationDepth))
    }

    val histogram = labelSummarizer.histogram
    val numInvalid = labelSummarizer.countInvalid
    val numFeatures = summarizer.mean.size
    val numFeaturesPlusIntercept = if (getFitIntercept) numFeatures + 1 else numFeatures
 
    val numClasses = MetadataUtils.getNumClasses(dataset.schema($(labelCol))) match {
      case Some(n: Int) =>
        require(n >= histogram.length, s"Specified number of classes $n was " +
          s"less than the number of unique labels ${histogram.length}.")
        n
      case None => histogram.length
    }
 
    val isMultinomial = $(family) match {
      case "binomial" =>
        require(numClasses == 1 || numClasses == 2, s"Binomial family only supports 1 or 2 " +
        s"outcome classes but found $numClasses.")
        false
      case "multinomial" => true
      case "auto" => numClasses > 2
      case other => throw new IllegalArgumentException(s"Unsupported family: $other")
    }
    val numCoefficientSets = if (isMultinomial) numClasses else 1
 
    if (isDefined(thresholds)) {
      require($(thresholds).length == numClasses, this.getClass.getSimpleName +
        ".train() called with non-matching numClasses and thresholds.length." +
        s" numClasses=$numClasses, but thresholds has length ${$(thresholds).length}")
    }
 
    instr.logNumClasses(numClasses)
    instr.logNumFeatures(numFeatures)

    val (coefficientMatrix, interceptVector, objectiveHistory) = {
      if (numInvalid != 0) {
        val msg = s"Classification labels should be in [0 to ${numClasses - 1}]. " +
          s"Found $numInvalid invalid labels."
        logError(msg)
        throw new SparkException(msg)
      }
 
      val isConstantLabel = histogram.count(_ != 0.0) == 1
 
      if ($(fitIntercept) && isConstantLabel) {
        logWarning(s"All labels are the same value and fitIntercept=true, so the coefficients " +
          s"will be zeros. Training is not needed.")
        val constantLabelIndex = Vectors.dense(histogram).argmax
        // TODO: use `compressed` after SPARK-17471
        val coefMatrix = if (numFeatures < numCoefficientSets) { new SparseMatrix(numCoefficientSets, numFeatures, Array.fill(numFeatures + 1)(0), Array.empty[Int], Array.empty[Double]) } else { new SparseMatrix(numCoefficientSets, numFeatures, Array.fill(numCoefficientSets + 1)(0), Array.empty[Int], Array.empty[Double], isTransposed = true) } val interceptVec = if (isMultinomial) { Vectors.sparse(numClasses, Seq((constantLabelIndex, Double.PositiveInfinity))) } else { Vectors.dense(if (numClasses == 2) Double.PositiveInfinity else Double.NegativeInfinity) } (coefMatrix, interceptVec, Array.empty[Double]) } else { if (!$(fitIntercept) && isConstantLabel) { logWarning(s"All labels belong to a single class and fitIntercept=false. It's a " + s"dangerous ground, so the algorithm may not converge.") } val featuresMean = summarizer.mean.toArray val featuresStd = summarizer.variance.toArray.map(math.sqrt) if (!$(fitIntercept) && (0 until numFeatures).exists { i =>
          featuresStd(i) == 0.0 && featuresMean(i) != 0.0 }) {
          logWarning("Fitting LogisticRegressionModel without intercept on dataset with " +
            "constant nonzero column, Spark MLlib outputs zero coefficients for constant " +
            "nonzero columns. This behavior is the same as R glmnet but different from LIBSVM.")
        }
 
        val regParamL1 = $(elasticNetParam) * $(regParam)
        val regParamL2 = (1.0 - $(elasticNetParam)) * $(regParam)
 
        val bcFeaturesStd = instances.context.broadcast(featuresStd)

        val costFun = new LogisticCostFun(instances, numClasses, $(fitIntercept),
          $(standardization), bcFeaturesStd, regParamL2, multinomial = isMultinomial,
          $(aggregationDepth))

/**
 * LogisticCostFun implements Breeze's DiffFunction[T] for a multinomial (softmax) logistic loss
 * function, as used in multi-class classification (it is also used in binary logistic regression).
 * It returns the loss and gradient with L2 regularization at a particular point (coefficients).
 * It's used in Breeze's convex optimization routines.
 */
private class LogisticCostFun(
    instances: RDD[Instance],
    numClasses: Int,
    fitIntercept: Boolean,
    standardization: Boolean,
    bcFeaturesStd: Broadcast[Array[Double]],
    regParamL2: Double,
    multinomial: Boolean,
    aggregationDepth: Int) extends DiffFunction[BDV[Double]] {
 
  override def calculate(coefficients: BDV[Double]): (Double, BDV[Double]) = {
    val coeffs = Vectors.fromBreeze(coefficients)
    val bcCoeffs = instances.context.broadcast(coeffs)
    val featuresStd = bcFeaturesStd.value
    val numFeatures = featuresStd.length
    val numCoefficientSets = if (multinomial) numClasses else 1
    val numFeaturesPlusIntercept = if (fitIntercept) numFeatures + 1 else numFeatures
 
    val logisticAggregator = {
      val seqOp = (c: LogisticAggregator, instance: Instance) => c.add(instance)
      val combOp = (c1: LogisticAggregator, c2: LogisticAggregator) => c1.merge(c2)
 
      instances.treeAggregate(
        new LogisticAggregator(bcCoeffs, bcFeaturesStd, numClasses, fitIntercept,
          multinomial)
      )(seqOp, combOp, aggregationDepth)
    }
 
    val totalGradientMatrix = logisticAggregator.gradient
    val coefMatrix = new DenseMatrix(numCoefficientSets, numFeaturesPlusIntercept, coeffs.toArray)
    // regVal is the sum of coefficients squares excluding intercept for L2 regularization.
    val regVal = if (regParamL2 == 0.0) {
      0.0
    } else {//如果正则参数L2不为0，那么会利用上一步产生的梯度矩阵来得到一个正则值来调整损失结果。
      var sum = 0.0
      coefMatrix.foreachActive { case (classIndex, featureIndex, value) =>
        // We do not apply regularization to the intercepts
        val isIntercept = fitIntercept && (featureIndex == numFeatures)
        if (!isIntercept) {
          // The following code will compute the loss of the regularization; also
          // the gradient of the regularization, and add back to totalGradientArray.
          sum += {
            if (standardization) {
              val gradValue = totalGradientMatrix(classIndex, featureIndex)
              totalGradientMatrix.update(classIndex, featureIndex, gradValue + regParamL2 * value)
              value * value
            } else {
              if (featuresStd(featureIndex) != 0.0) {
                // If `standardization` is false, we still standardize the data
                // to improve the rate of convergence; as a result, we have to
                // perform this reverse standardization by penalizing each component
                // differently to get effectively the same objective function when
                // the training dataset is not standardized.
                val temp = value / (featuresStd(featureIndex) * featuresStd(featureIndex))
                val gradValue = totalGradientMatrix(classIndex, featureIndex)
                totalGradientMatrix.update(classIndex, featureIndex, gradValue + regParamL2 * temp)
                value * temp
              } else {
                0.0
              }
            }
          }
        }
      }
      0.5 * regParamL2 * sum
    }
    bcCoeffs.destroy(blocking = false)
 
    (logisticAggregator.loss + regVal, new BDV(totalGradientMatrix.toArray))
  }
}

private class LogisticAggregator(
    bcCoefficients: Broadcast[Vector],
    bcFeaturesStd: Broadcast[Array[Double]],
    numClasses: Int,
    fitIntercept: Boolean,
    multinomial: Boolean) extends Serializable with Logging {
 
  private val numFeatures = bcFeaturesStd.value.length
  private val numFeaturesPlusIntercept = if (fitIntercept) numFeatures + 1 else numFeatures
  private val coefficientSize = bcCoefficients.value.size
  private val numCoefficientSets = if (multinomial) numClasses else 1
  if (multinomial) {
    require(numClasses ==  coefficientSize / numFeaturesPlusIntercept, s"The number of " +
      s"coefficients should be ${numClasses * numFeaturesPlusIntercept} but was $coefficientSize")
  } else {
    require(coefficientSize == numFeaturesPlusIntercept, s"Expected $numFeaturesPlusIntercept " +
      s"coefficients but got $coefficientSize")
    require(numClasses == 1 || numClasses == 2, s"Binary logistic aggregator requires numClasses " +
      s"in {1, 2} but found $numClasses.")
  }
 
  private var weightSum = 0.0
  private var lossSum = 0.0
 
  private val gradientSumArray = Array.ofDim[Double](coefficientSize)
 
  if (multinomial && numClasses <= 2) { logInfo(s"Multinomial logistic regression for binary classification yields separate " + s"coefficients for positive and negative classes. When no regularization is applied, the" + s"result will be effectively the same as binary logistic regression. When regularization" + s"is applied, multinomial loss will produce a result different from binary loss.") } /** Update gradient and loss using binary loss function. */ private def binaryUpdateInPlace( features: Vector, weight: Double, label: Double): Unit = { val localFeaturesStd = bcFeaturesStd.value val localCoefficients = bcCoefficients.value val localGradientArray = gradientSumArray val margin = - {//如果值不为0，则sum为系数×值/标准差 var sum = 0.0 features.foreachActive { (index, value) =>
        if (localFeaturesStd(index) != 0.0 && value != 0.0) {
          sum += localCoefficients(index) * value / localFeaturesStd(index)
        }
      }//如果有截距，加上截距偏移
      if (fitIntercept) sum += localCoefficients(numFeaturesPlusIntercept - 1)
      sum
    }
//这儿计算梯度矩阵
    val multiplier = weight * (1.0 / (1.0 + math.exp(margin)) - label)
 
    features.foreachActive { (index, value) =>
      if (localFeaturesStd(index) != 0.0 && value != 0.0) {
        localGradientArray(index) += multiplier * value / localFeaturesStd(index)
      }
    }
 
    if (fitIntercept) {
      localGradientArray(numFeaturesPlusIntercept - 1) += multiplier
    }
 
    if (label > 0) {
      // The following is equivalent to log(1 + exp(margin)) but more numerically stable.
      lossSum += weight * MLUtils.log1pExp(margin)
    } else {
      lossSum += weight * (MLUtils.log1pExp(margin) - margin)
    }
  }
 
  /** Update gradient and loss using multinomial (softmax) loss function. */
  private def multinomialUpdateInPlace(
      features: Vector,
      weight: Double,
      label: Double): Unit = {
    // TODO: use level 2 BLAS operations
    /*
      Note: this can still be used when numClasses = 2 for binary
      logistic regression without pivoting.
     */
    val localFeaturesStd = bcFeaturesStd.value
    val localCoefficients = bcCoefficients.value
    val localGradientArray = gradientSumArray
 
    // marginOfLabel is margins(label) in the formula
    var marginOfLabel = 0.0
    var maxMargin = Double.NegativeInfinity
 
    val margins = new Array[Double](numClasses)
    features.foreachActive { (index, value) =>
      val stdValue = value / localFeaturesStd(index)
      var j = 0
      while (j < numClasses) {
        margins(j) += localCoefficients(index * numClasses + j) * stdValue
        j += 1
      }
    }
    var i = 0
    while (i < numClasses) { if (fitIntercept) { margins(i) += localCoefficients(numClasses * numFeatures + i) } if (i == label.toInt) marginOfLabel = margins(i) if (margins(i) > maxMargin) {
        maxMargin = margins(i)
      }
      i += 1
    }
 
    /**
     * When maxMargin > 0, the original formula could cause overflow.
     * We address this by subtracting maxMargin from all the margins, so it's guaranteed
     * that all of the new margins will be smaller than zero to prevent arithmetic overflow.
     */
    val multipliers = new Array[Double](numClasses)
    val sum = {
      var temp = 0.0
      var i = 0
      while (i < numClasses) { if (maxMargin > 0) margins(i) -= maxMargin
        val exp = math.exp(margins(i))
        temp += exp
        multipliers(i) = exp
        i += 1
      }
      temp
    }
 
    margins.indices.foreach { i =>
      multipliers(i) = multipliers(i) / sum - (if (label == i) 1.0 else 0.0)
    }
    features.foreachActive { (index, value) =>
      if (localFeaturesStd(index) != 0.0 && value != 0.0) {
        val stdValue = value / localFeaturesStd(index)
        var j = 0
        while (j < numClasses) {
          localGradientArray(index * numClasses + j) +=
            weight * multipliers(j) * stdValue
          j += 1
        }
      }
    }
    if (fitIntercept) {
      var i = 0
      while (i < numClasses) { localGradientArray(numFeatures * numClasses + i) += weight * multipliers(i) i += 1 } } val loss = if (maxMargin > 0) {
      math.log(sum) - marginOfLabel + maxMargin
    } else {
      math.log(sum) - marginOfLabel
    }
    lossSum += weight * loss
  }
 
  /**
   * Add a new training instance to this LogisticAggregator, and update the loss and gradient
   * of the objective function.
   *
   * @param instance The instance of data point to be added.
   * @return This LogisticAggregator object.
   */
  def add(instance: Instance): this.type = {
    instance match { case Instance(label, weight, features) =>
      require(numFeatures == features.size, s"Dimensions mismatch when adding new instance." +
        s" Expecting $numFeatures but got ${features.size}.")
      require(weight >= 0.0, s"instance weight, $weight has to be >= 0.0")
 
      if (weight == 0.0) return this
 
      if (multinomial) {
        multinomialUpdateInPlace(features, weight, label)
      } else {
        binaryUpdateInPlace(features, weight, label)
      }
      weightSum += weight
      this
    }
  }
 
  /**
   * Merge another LogisticAggregator, and update the loss and gradient
   * of the objective function.
   * (Note that it's in place merging; as a result, `this` object will be modified.)
   *
   * @param other The other LogisticAggregator to be merged.
   * @return This LogisticAggregator object.
   */
  def merge(other: LogisticAggregator): this.type = {
    require(numFeatures == other.numFeatures, s"Dimensions mismatch when merging with another " +
      s"LeastSquaresAggregator. Expecting $numFeatures but got ${other.numFeatures}.")
 
    if (other.weightSum != 0.0) {
      weightSum += other.weightSum
      lossSum += other.lossSum
 
      var i = 0
      val localThisGradientSumArray = this.gradientSumArray
      val localOtherGradientSumArray = other.gradientSumArray
      val len = localThisGradientSumArray.length
      while (i < len) { localThisGradientSumArray(i) += localOtherGradientSumArray(i) i += 1 } } this } def loss: Double = { require(weightSum > 0.0, s"The effective number of instances should be " +
      s"greater than 0.0, but $weightSum.")
    lossSum / weightSum
  }
 
  def gradient: Matrix = {
    require(weightSum > 0.0, s"The effective number of instances should be " +
      s"greater than 0.0, but $weightSum.")
    val result = Vectors.dense(gradientSumArray.clone())
    scal(1.0 / weightSum, result)
    new DenseMatrix(numCoefficientSets, numFeaturesPlusIntercept, result.toArray)
  }
}

        val optimizer = if ($(elasticNetParam) == 0.0 || $(regParam) == 0.0) {
          new BreezeLBFGS[BDV[Double]]($(maxIter), 10, $(tol))
        } else {
          val standardizationParam = $(standardization)
          def regParamL1Fun = (index: Int) => {
            // Remove the L1 penalization on the intercept
            val isIntercept = $(fitIntercept) && index >= numFeatures * numCoefficientSets
            if (isIntercept) {
              0.0
            } else {
              if (standardizationParam) {
                regParamL1
              } else {
                val featureIndex = index / numCoefficientSets
                // If `standardization` is false, we still standardize the data
                // to improve the rate of convergence; as a result, we have to
                // perform this reverse standardization by penalizing each component
                // differently to get effectively the same objective function when
                // the training dataset is not standardized.
                if (featuresStd(featureIndex) != 0.0) {
                  regParamL1 / featuresStd(featureIndex)
                } else {
                  0.0
                }
              }
            }
          }
          new BreezeOWLQN[Int, BDV[Double]]($(maxIter), 10, regParamL1Fun, $(tol))
        }
 
        /*
          The coefficients are laid out in column major order during training. Here we initialize
          a column major matrix of initial coefficients.
         */
        val initialCoefWithInterceptMatrix =
          Matrices.zeros(numCoefficientSets, numFeaturesPlusIntercept)
 
        val initialModelIsValid = optInitialModel match {
          case Some(_initialModel) =>
            val providedCoefs = _initialModel.coefficientMatrix
            val modelIsValid = (providedCoefs.numRows == numCoefficientSets) &&
              (providedCoefs.numCols == numFeatures) &&
              (_initialModel.interceptVector.size == numCoefficientSets) &&
              (_initialModel.getFitIntercept == $(fitIntercept))
            if (!modelIsValid) {
              logWarning(s"Initial coefficients will be ignored! Its dimensions " +
                s"(${providedCoefs.numRows}, ${providedCoefs.numCols}) did not match the " +
                s"expected size ($numCoefficientSets, $numFeatures)")
            }
            modelIsValid
          case None => false
        }
 
        if (initialModelIsValid) {
          val providedCoef = optInitialModel.get.coefficientMatrix
          providedCoef.foreachActive { (classIndex, featureIndex, value) =>
            // We need to scale the coefficients since they will be trained in the scaled space
            initialCoefWithInterceptMatrix.update(classIndex, featureIndex,
              value * featuresStd(featureIndex))
          }
          if ($(fitIntercept)) {
            optInitialModel.get.interceptVector.foreachActive { (classIndex, value) =>
              initialCoefWithInterceptMatrix.update(classIndex, numFeatures, value)
            }
          }
        } else if ($(fitIntercept) && isMultinomial) {
          /*
             For multinomial logistic regression, when we initialize the coefficients as zeros,
             it will converge faster if we initialize the intercepts such that
             it follows the distribution of the labels.
             {{{
               P(1) = \exp(b_1) / Z
               ...
               P(K) = \exp(b_K) / Z
               where Z = \sum_{k=1}^{K} \exp(b_k)
             }}}
             Since this doesn't have a unique solution, one of the solutions that satisfies the
             above equations is
             {{{
               \exp(b_k) = count_k * \exp(\lambda)
               b_k = \log(count_k) * \lambda
             }}}
             \lambda is a free parameter, so choose the phase \lambda such that the
             mean is centered. This yields
             {{{
               b_k = \log(count_k)
               b_k' = b_k - \mean(b_k)
             }}}
           */
          val rawIntercepts = histogram.map(c => math.log(c + 1)) // add 1 for smoothing
          val rawMean = rawIntercepts.sum / rawIntercepts.length
          rawIntercepts.indices.foreach { i =>
            initialCoefWithInterceptMatrix.update(i, numFeatures, rawIntercepts(i) - rawMean)
          }
        } else if ($(fitIntercept)) {
          /*
             For binary logistic regression, when we initialize the coefficients as zeros,
             it will converge faster if we initialize the intercept such that
             it follows the distribution of the labels.
 
             {{{
               P(0) = 1 / (1 + \exp(b)), and
               P(1) = \exp(b) / (1 + \exp(b))
             }}}, hence
             {{{
               b = \log{P(1) / P(0)} = \log{count_1 / count_0}
             }}}
           */
          initialCoefWithInterceptMatrix.update(0, numFeatures,
            math.log(histogram(1) / histogram(0)))
        }

        val states = optimizer.iterations(new CachedDiffFunction(costFun),
          new BDV[Double](initialCoefWithInterceptMatrix.toArray))
 
        /*
           Note that in Logistic Regression, the objective history (loss + regularization)
           is log-likelihood which is invariant under feature standardization. As a result,
           the objective history from optimizer is the same as the one in the original space.
         */
        val arrayBuilder = mutable.ArrayBuilder.make[Double]
        var state: optimizer.State = null
        while (states.hasNext) {
          state = states.next()
          arrayBuilder += state.adjustedValue
        }
        bcFeaturesStd.destroy(blocking = false)
 
        if (state == null) {
          val msg = s"${optimizer.getClass.getName} failed."
          logError(msg)
          throw new SparkException(msg)
        }
 
        /*
           The coefficients are trained in the scaled space; we're converting them back to
           the original space.
 
           Additionally, since the coefficients were laid out in column major order during training
           to avoid extra computation, we convert them back to row major before passing them to the
           model.
 
           Note that the intercept in scaled space and original space is the same;
           as a result, no scaling is needed.
         */
        val allCoefficients = state.x.toArray.clone()
        val allCoefMatrix = new DenseMatrix(numCoefficientSets, numFeaturesPlusIntercept,
          allCoefficients)
        val denseCoefficientMatrix = new DenseMatrix(numCoefficientSets, numFeatures,
          new Array[Double](numCoefficientSets * numFeatures), isTransposed = true)
        val interceptVec = if ($(fitIntercept) || !isMultinomial) {
          Vectors.zeros(numCoefficientSets)
        } else {
          Vectors.sparse(numCoefficientSets, Seq())
        }
        // separate intercepts and coefficients from the combined matrix
        allCoefMatrix.foreachActive { (classIndex, featureIndex, value) =>
          val isIntercept = $(fitIntercept) && (featureIndex == numFeatures)
          if (!isIntercept && featuresStd(featureIndex) != 0.0) {
            denseCoefficientMatrix.update(classIndex, featureIndex,
              value / featuresStd(featureIndex))
          }
          if (isIntercept) interceptVec.toArray(classIndex) = value
        }
 
        if ($(regParam) == 0.0 && isMultinomial) {
          /*
            When no regularization is applied, the multinomial coefficients lack identifiability
            because we do not use a pivot class. We can add any constant value to the coefficients
            and get the same likelihood. So here, we choose the mean centered coefficients for
            reproducibility. This method follows the approach in glmnet, described here:
 
            Friedman, et al. "Regularization Paths for Generalized Linear Models via
              Coordinate Descent," https://core.ac.uk/download/files/153/6287975.pdf
           */
          val denseValues = denseCoefficientMatrix.values
          val coefficientMean = denseValues.sum / denseValues.length
          denseCoefficientMatrix.update(_ - coefficientMean)
        }
 
        // TODO: use `denseCoefficientMatrix.compressed` after SPARK-17471
        val compressedCoefficientMatrix = if (isMultinomial) {
          denseCoefficientMatrix
        } else {
          val compressedVector = Vectors.dense(denseCoefficientMatrix.values).compressed
          compressedVector match {
            case dv: DenseVector => denseCoefficientMatrix
            case sv: SparseVector =>
              new SparseMatrix(1, numFeatures, Array(0, sv.indices.length), sv.indices, sv.values,
                isTransposed = true)
          }
        }
 
        // center the intercepts when using multinomial algorithm
        if ($(fitIntercept) && isMultinomial) {
          val interceptArray = interceptVec.toArray
          val interceptMean = interceptArray.sum / interceptArray.length
          (0 until interceptVec.size).foreach { i => interceptArray(i) -= interceptMean }
        }
        (compressedCoefficientMatrix, interceptVec.compressed, arrayBuilder.result())
      }
    }
 
    if (handlePersistence) instances.unpersist()
 
    val model = copyValues(new LogisticRegressionModel(uid, coefficientMatrix, interceptVector,
      numClasses, isMultinomial))
    // TODO: implement summary model for multinomial case
    val m = if (!isMultinomial) {
      val (summaryModel, probabilityColName) = model.findSummaryModelAndProbabilityCol()
      val logRegSummary = new BinaryLogisticRegressionTrainingSummary(
        summaryModel.transform(dataset),
        probabilityColName,
        $(labelCol),
        $(featuresCol),
        objectiveHistory)
      model.setSummary(Some(logRegSummary))
    } else {
      model
    }
    instr.logSuccess(m)
    m
  }

  def iterations(f: DF, init: T): Iterator[State] = {
    val adjustedFun = adjustFunction(f)
    infiniteIterations(f, initialState(adjustedFun, init)).takeUpToWhere{s =>
      convergenceCheck.apply(s, s.convergenceInfo) match {
        case Some(converged) =>
          logger.info(s"Converged because ${converged.reason}")
          true
        case None =>
          false
      }
    }
  }

  def infiniteIterations(f: DF, state: State): Iterator[State] = {
    var failedOnce = false
    val adjustedFun = adjustFunction(f)
 
    Iterator.iterate(state) { state => try {
        val dir = chooseDescentDirection(state, adjustedFun)//选择下降方向
        val stepSize = determineStepSize(state, adjustedFun, dir)//决定步长，这里利用强Wolfe准则来计算
        logger.info(f"Step Size: $stepSize%.4g")
        val x = takeStep(state,dir,stepSize)//得到新的计算后的X值
        val (value,grad) = calculateObjective(adjustedFun, x, state.history)
        val (adjValue,adjGrad) = adjust(x,grad,value)//得到调整值
        val oneOffImprovement = (state.adjustedValue - adjValue)/(state.adjustedValue.abs max adjValue.abs max 1E-6 * state.initialAdjVal.abs)
        logger.info(f"Val and Grad Norm: $adjValue%.6g (rel: $oneOffImprovement%.3g) ${norm(adjGrad)}%.6g")
        val history = updateHistory(x,grad,value, adjustedFun, state)
        val newCInfo = convergenceCheck.update(x, grad, value, state, state.convergenceInfo)//更新x值，即更新系数矩阵
        failedOnce = false
        FirstOrderMinimizer.State(x, value, grad, adjValue, adjGrad, state.iter + 1, state.initialAdjVal, history, newCInfo)
    } catch {
        case x: FirstOrderException if !failedOnce =>
          failedOnce = true
          logger.error("Failure! Resetting history: " + x)
          state.copy(history = initialHistory(adjustedFun, state.x))
        case x: FirstOrderException =>
          logger.error("Failure again! Giving up and returning. Maybe the objective is just poorly behaved?")
          state.copy(searchFailed = true)
      }
    }
  }

class LBFGS[T](convergenceCheck: ConvergenceCheck[T], m: Int)(implicit space: MutableInnerProductModule[T, Double]) extends FirstOrderMinimizer[T, DiffFunction[T]](convergenceCheck) with SerializableLogging {
 
  def this(maxIter: Int = -1, m: Int=7, tolerance: Double=1E-9)
          (implicit space: MutableInnerProductModule[T, Double]) = this(FirstOrderMinimizer.defaultConvergenceCheck(maxIter, tolerance), m )
......
 
  /**
   * Given a direction, perform a line search to find 
   * a direction to descend. At the moment, this just executes
   * backtracking, so it does not fulfill the wolfe conditions.
   *
   * @param state the current state
   * @param f The objective
   * @param dir The step direction
   * @return stepSize
   */
  protected def determineStepSize(state: State, f: DiffFunction[T], dir: T) = {
    val x = state.x
    val grad = state.grad
 
    val ff = LineSearch.functionFromSearchDirection(f, x, dir)
    val search = new StrongWolfeLineSearch(maxZoomIter = 10, maxLineSearchIter = 10) // TODO: Need good default values here.
    val alpha = search.minimize(ff, if(state.iter == 0.0) 1.0/norm(dir) else 1.0)
 
    if(alpha * norm(grad) < 1E-10)
      throw new StepSizeUnderflow
    alpha
  }
}

/*
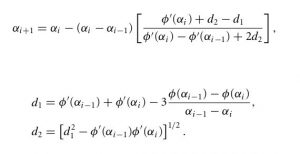
package breeze.optimize
 
import breeze.util.SerializableLogging
 
abstract class CubicLineSearch extends SerializableLogging with MinimizingLineSearch {
  import scala.math._
 
  case class Bracket(
    t: Double, // 1d line search parameter
    dd: Double, // Directional Derivative at t
    fval: Double // Function value at t
    )
 
  /*
   * Invoke line search, returning stepsize
   */
  def minimize(f: DiffFunction[Double], init: Double = 1.0): Double
  /*
   * Cubic interpolation to find the minimum inside the bracket l and r.
   * Uses the fval and gradient at the left and right side, which gives
   * the four bits of information required to interpolate a cubic.
   * This is additionally "safe-guarded" whereby steps too close to
   * either side of the interval will not be selected.
   */
  def interp(l: Bracket, r: Bracket) = {
    // See N&W p57 actual for an explanation of the math
    val d1 = l.dd + r.dd - 3 * (l.fval - r.fval) / (l.t - r.t)
    val d2 = sqrt(d1 * d1 - l.dd * r.dd)
    val multipler = r.t - l.t
    val t = r.t - multipler * (r.dd + d2 - d1) / (r.dd - l.dd + 2 * d2)
 
    // If t is too close to either end bracket, move it closer to the middle
 
    val lbound = l.t + 0.1 * (r.t - l.t)
    val ubound = l.t + 0.9 * (r.t - l.t)
    t match {
      case _ if t < lbound =>
        logger.debug("Cubic " + t + " below LHS limit: " + lbound)
        lbound
      case _ if t > ubound =>
        logger.debug("Cubic " + t + " above RHS limit: " + ubound)
        ubound
      case _ => t
    }
  }
}
 
/*
 * This line search will attempt steps larger than step length one,
 * unlike back-tracking line searches. It also comes with strong convergence
 * properties. It selects step lengths using cubic interpolation, which
 * works better than other approaches in my experience.
 * Based on Nocedal & Wright.
 */
class StrongWolfeLineSearch(maxZoomIter: Int, maxLineSearchIter: Int) extends CubicLineSearch {
  import scala.math._
 
  val c1 = 1e-4
  val c2 = 0.9
 
  /**
   * Performs a line search on the function f, returning a point satisfying
   * the Strong Wolfe conditions. Based on the line search detailed in
   * Nocedal & Wright Numerical Optimization p58.
   */
  def minimize(f: DiffFunction[Double], init: Double = 1.0):Double = {
 
    def phi(t: Double): Bracket = {
      val (pval, pdd) = f.calculate(t)
      Bracket(t = t, dd = pdd, fval = pval)
    }
 
    var t = init // Search's current multiple of pk
    var low = phi(0.0)
    val fval = low.fval
    val dd = low.dd
 
    if (dd > 0) {
      throw new FirstOrderException("Line search invoked with non-descent direction: " + dd)
    }
 
    /**
     * Assuming a point satisfying the strong wolfe conditions exists within
     * the passed interval, this method finds it by iteratively refining the
     * interval. Nocedal & Wright give the following invariants for zoom's loop:
     *
     *  - The interval bounded by low.t and hi.t contains a point satisfying the
     *    strong Wolfe conditions.
     *  - Among all points evaluated so far that satisfy the "sufficient decrease"
     *    condition, low.t is the one with the smallest fval.
     *  - hi.t is chosen so that low.dd * (hi.t - low.t) < 0.
     */
    def zoom(linit: Bracket, rinit: Bracket): Double = {
 
      var low = linit
      var hi = rinit
 
      for (i <- 0 until maxZoomIter) {
        // Interp assumes left less than right in t value, so flip if needed
        val t = if (low.t > hi.t) interp(hi, low) else interp(low, hi)
 
        // Evaluate objective at t, and build bracket
        val c = phi(t)
        //logger.debug("ZOOM:\n c: " + c + " \n l: " + low + " \nr: " + hi)
        logger.info("Line search t: " + t + " fval: " + c.fval +
          " rhs: " + (fval + c1 * c.t * dd) + " cdd: " + c.dd)
 
        ///////////////
        /// Update left or right bracket, or both
 
        if (c.fval > fval + c1 * c.t * dd || c.fval >= low.fval) {
          // "Sufficient decrease" condition not satisfied by c. Shrink interval at right
          hi = c
          logger.debug("hi=c")
        } else {
 
          // Zoom exit condition is the "curvature" condition
          // Essentially that the directional derivative is large enough
          if (abs(c.dd) <= c2 * abs(dd)) {
            return c.t
          }
 
          // If the signs don't coincide, flip left to right before updating l to c
          if (c.dd * (hi.t - low.t) >= 0) {
            logger.debug("flipping")
            hi = low
          }
 
          logger.debug("low=c")
          // If curvature condition not satisfied, move the left hand side of the
          // interval further away from t=0.
          low = c
        }
      }
 
      throw new FirstOrderException(s"Line search zoom failed")
    }
 
    ///////////////////////////////////////////////////////////////////
 
    for (i <- 0 until maxLineSearchIter) {
      val c = phi(t)
 
      // If phi has a bounded domain, inf or nan usually indicates we took
      // too large a step.
      if (java.lang.Double.isInfinite(c.fval) || java.lang.Double.isNaN(c.fval)) {
        t /= 2.0
        logger.error("Encountered bad values in function evaluation. Decreasing step size to " + t)
      } else {
 
        // Zoom if "sufficient decrease" condition is not satisfied
        if ((c.fval > fval + c1 * t * dd) ||
          (c.fval >= low.fval && i > 0)) {
          logger.debug("Line search t: " + t + " fval: " + c.fval + " cdd: " + c.dd)
          return zoom(low, c)
        }
 
        // We don't need to zoom at all
        // if the strong wolfe condition is satisfied already.
        if (abs(c.dd) <= c2 * abs(dd)) {
          return c.t
        }
 
        // If c.dd is positive, we zoom on the inverted interval.
        // Occurs if we skipped over the nearest local minimum
        // over to the next one.
        if (c.dd >= 0) {
          logger.debug("Line search t: " + t + " fval: " + c.fval +
            " rhs: " + (fval + c1 * t * dd) + " cdd: " + c.dd)
          return zoom(c, low)
        }
 
        low = c
        t *= 1.5
        logger.debug("Sufficent Decrease condition but not curvature condition satisfied. Increased t to: " + t)
      }
    }
 
    throw new FirstOrderException("Line search failed")
  }
 
}