原创文章,转载请注明: 转载自慢慢的回味
本文链接地址: NaiveBayes(朴素贝叶斯) in ML
贝叶斯定理例子
以《数据挖掘导论》里面的例子开始:
考虑两个主球队比赛:队0和队1,如果队0的胜率为65%,队1为35%。队0获胜时队1为主场为30%,而队1取胜的比赛中75%是在主场。问:下一场比赛在队1的主场进行,哪个队最有可能胜出呢?
这儿以贝叶斯定理来解答:
假设X,Y是一对随机变量,令X代表主场,Y代表胜利者。X、Y的取值范围为『0,1』。X=0表示队0,X=1表示队1,Y=0表示失败,Y=1表示胜利,则:
队0取胜的先验概率:P(Y=0)= 0.65,
队0取胜的先验概率:P(Y=1)= 0.35,
队1取胜的比赛中在主场的条件概率:P(X=1|Y=1)=0.75,
队0获胜时队1为主场的条件概率:P(X=1|Y=0)=0.3。
现在需要计算队1为主场的条件概率,即P(Y=1|X=1)和P(Y=0|X=1):
贝叶斯定理为:![]()
则:
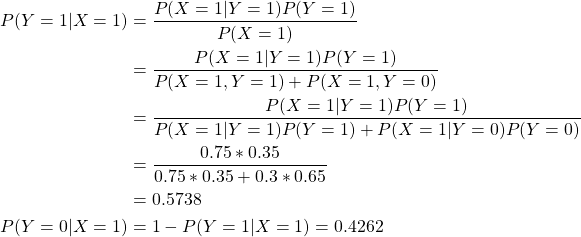
所以队1更能赢得比赛。
朴素贝叶斯
朴素贝叶斯就是指类条件是独立的,即
![Rendered by QuickLaTeX.com \[ P(X|Y=y) = \prod_{i=1}^d P(X_i|Y=y) \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-46d41c8f727e5d51803e08a400dd7359_l3.png)
其中,![]() 条件独立。
条件独立。
设![]() 为一个待分类项,f就是X的一个特征(feature), 取值范围0
为一个待分类项,f就是X的一个特征(feature), 取值范围0![]()
现在就需要计算![]() 就可以了,即样本X属于每个分类的条件概率。
就可以了,即样本X属于每个分类的条件概率。
由贝叶斯定理有:
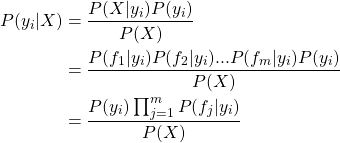
在下面的代码中,对应的变量为:

其中sumTermFreqs(j)表示分类i中特征j的词频,sumTermFreqs.values.sum表示分类i中词频之和,n为分类i的文档数,numDocuments为总的文档数,P(y_i)为分类i的先验概率,P(f_j|y_i)为特征j为分类i的条件概率,lambda为平滑参数,也可防止分类i或特征j缺少样本而分子为零。
代码分析
test("Naive Bayes Multinomial") { val nPoints = 1000 val piArray = Array(0.5, 0.1, 0.4).map(math.log) val thetaArray = Array( Array(0.70, 0.10, 0.10, 0.10), // label 0 Array(0.10, 0.70, 0.10, 0.10), // label 1 Array(0.10, 0.10, 0.70, 0.10) // label 2 ).map(_.map(math.log)) val pi = Vectors.dense(piArray) val theta = new DenseMatrix(3, 4, thetaArray.flatten, true) val testDataset = generateNaiveBayesInput(piArray, thetaArray, nPoints, 42, "multinomial").toDF() val nb = new NaiveBayes().setSmoothing(1.0).setModelType("multinomial") val model = nb.fit(testDataset) validateModelFit(pi, theta, model) assert(model.hasParent) val validationDataset = generateNaiveBayesInput(piArray, thetaArray, nPoints, 17, "multinomial").toDF() val predictionAndLabels = model.transform(validationDataset).select("prediction", "label") validatePrediction(predictionAndLabels) val featureAndProbabilities = model.transform(validationDataset) .select("features", "probability") validateProbabilities(featureAndProbabilities, model, "multinomial") } |
override def fit(dataset: Dataset[_]): M = { // This handles a few items such as schema validation. // Developers only need to implement train(). transformSchema(dataset.schema, logging = true) // Cast LabelCol to DoubleType and keep the metadata. val labelMeta = dataset.schema($(labelCol)).metadata val casted = dataset.withColumn($(labelCol), col($(labelCol)).cast(DoubleType), labelMeta) copyValues(train(casted).setParent(this)) } |
override protected def train(dataset: Dataset[_]): NaiveBayesModel = { trainWithLabelCheck(dataset, positiveLabel = true) } /** * ml assumes input labels in range [0, numClasses). But this implementation * is also called by mllib NaiveBayes which allows other kinds of input labels * such as {-1, +1}. `positiveLabel` is used to determine whether the label * should be checked and it should be removed when we remove mllib NaiveBayes. */ private[spark] def trainWithLabelCheck( dataset: Dataset[_], positiveLabel: Boolean): NaiveBayesModel = { if (positiveLabel) { val numClasses = getNumClasses(dataset) if (isDefined(thresholds)) { require($(thresholds).length == numClasses, this.getClass.getSimpleName + ".train() called with non-matching numClasses and thresholds.length." + s" numClasses=$numClasses, but thresholds has length ${$(thresholds).length}") } } val modelTypeValue = $(modelType) val requireValues: Vector => Unit = { modelTypeValue match { case Multinomial => requireNonnegativeValues case Bernoulli => requireZeroOneBernoulliValues case _ => // This should never happen. throw new UnknownError(s"Invalid modelType: ${$(modelType)}.") } } val numFeatures = dataset.select(col($(featuresCol))).head().getAs[Vector](0).size val w = if (!isDefined(weightCol) || $(weightCol).isEmpty) lit(1.0) else col($(weightCol)) // Aggregates term frequencies per label. // TODO: Calling aggregateByKey and collect creates two stages, we can implement something // TODO: similar to reduceByKeyLocally to save one stage. val aggregated = dataset.select(col($(labelCol)), w, col($(featuresCol))).rdd .map { row => (row.getDouble(0), (row.getDouble(1), row.getAs[Vector](2))) }.aggregateByKey[(Double, DenseVector)]((0.0, Vectors.zeros(numFeatures).toDense))( seqOp = { case ((weightSum: Double, featureSum: DenseVector), (weight, features)) => requireValues(features) BLAS.axpy(weight, features, featureSum) (weightSum + weight, featureSum) }, combOp = { case ((weightSum1, featureSum1), (weightSum2, featureSum2)) => BLAS.axpy(1.0, featureSum2, featureSum1) (weightSum1 + weightSum2, featureSum1) }).collect().sortBy(_._1) val numLabels = aggregated.length val numDocuments = aggregated.map(_._2._1).sum val labelArray = new Array[Double](numLabels) val piArray = new Array[Double](numLabels) val thetaArray = new Array[Double](numLabels * numFeatures) val lambda = $(smoothing) val piLogDenom = math.log(numDocuments + numLabels * lambda) var i = 0 aggregated.foreach { case (label, (n, sumTermFreqs)) => labelArray(i) = label piArray(i) = math.log(n + lambda) - piLogDenom val thetaLogDenom = $(modelType) match { case Multinomial => math.log(sumTermFreqs.values.sum + numFeatures * lambda) case Bernoulli => math.log(n + 2.0 * lambda) case _ => // This should never happen. throw new UnknownError(s"Invalid modelType: ${$(modelType)}.") } var j = 0 while (j < numFeatures) { thetaArray(i * numFeatures + j) = math.log(sumTermFreqs(j) + lambda) - thetaLogDenom j += 1 } i += 1 } val pi = Vectors.dense(piArray) val theta = new DenseMatrix(numLabels, numFeatures, thetaArray, true) new NaiveBayesModel(uid, pi, theta).setOldLabels(labelArray) } |
本作品采用知识共享署名 4.0 国际许可协议进行许可。