原创文章,转载请注明: 转载自慢慢的回味
本文链接地址: Tensorflow Embedding原理
Embedding(嵌入)指的是把低维的流形嵌入到高维空间中。举个简单的例子,三维空间的球体(地球)是一个二维流形嵌入在三维空间(欧几里得空间),即地球上的任意一个点只需一个二维的经纬度就可以表达,但三维空间中用x,y,z。深度学习领域假设“自然的原始数据是低维的流形嵌入到原始数据所在的高维空间中”。所以,深度学习的过程就是把高维原始数据(图像,句子)再回映射到低维流形中,从而是数据变得可分,而这个映射就叫嵌入(Embedding)。比如文档Embedding,就是把每篇文档所组成的单词映射到一个低维的表征向量,使得每篇文档可以用一个表征向量来表示,即Embedding就是从原始数据提取出来的Feature,也就是通过神经网络映射之后的低维向量。
如下例子,蓝色曲线和红色曲线是无法线性可分的(图二),只能用非线性函数分离(图三),但真实的数据中却很难找到这样的非线性函数,但通过对数据进行Embedding过程进行映射后(图四),就可以线性可分了。

文档Embedding原理
在对文本进行分类的过程中,第一步便是需要对文本样本进行降维,比如文本字库大小为10000,不能用10000列队矩阵来进行全连接计算,由于每个样本大概只占300个单词的稀疏向量,所以我们可以用一个列数更少的致密向量来代替每个样本,即可以用300个Embedding向量来对所有的文档进行低维映射。
Embedding方法就是用来把文本样本的稀疏矩阵转换为致密矩阵的一个方法。
假设有如下的矩阵乘法:
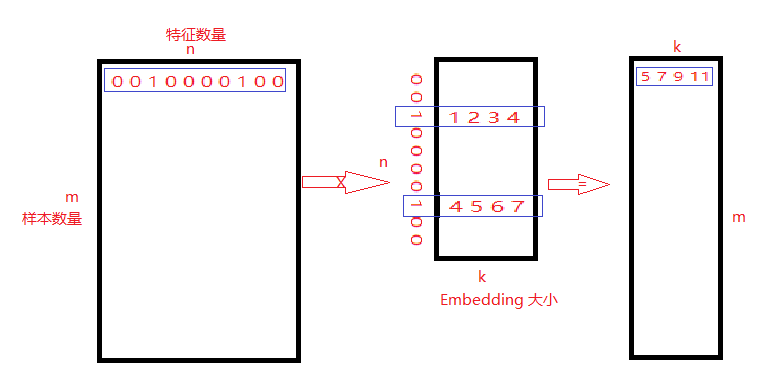
一个由m个文本样本,每个样本由n个特征构成的稀疏向量,组成的样本库。每个样本中含有的单词用1表示,比如第一个样本有2个单词。
现在构建一个Embedding矩阵,大小为n * k。其中Embedding矩阵的值可以用uniform方法进行随机初始化。
用样本中对应1的位置进行Embedding向量选择,然后相加,得到最终的向量 [5 7 9 11]。这样,m * n 的稀疏矩阵就变成了 m * k 的致密矩阵了。
测试程序
现在用一个示例程序来测试Tensorflow中Embedding API:
''' Created on Jul 10, 2019 @author: root ''' from __future__ import absolute_import, division, print_function, unicode_literals import tensorflow as tf from tensorflow.python.ops import embedding_ops import numpy as np a = tf.Variable(np.arange(8).reshape(2,4)) b = tf.Variable(np.arange(8,16).reshape(2,4)) c = tf.Variable(np.arange(16, 24).reshape(2,4)) embedded_tensor = embedding_ops.embedding_lookup(params=[a,b,c], ids=[1,2,4,3], partition_strategy='mod', name="embedding") print (a) print (b) print (c) print ("########## embedded_tensor #########") print(embedded_tensor) # 1 0 4 0 # 0 2 1 0 # 3 0 0 5 sparse_tensor = tf.SparseTensor(indices=[[0,0],[0,2],[1,1],[1,2],[2,0],[2,3]], values=[1,4,2,1,3,5], dense_shape=[3,4]) embedded_sparse_tensor = embedding_ops.embedding_lookup_sparse(params=[a,b,c], sp_ids=sparse_tensor, sp_weights=None, partition_strategy='mod', name="embedding", combiner="sum") print ("########## embedded_sparse_tensor #########") print(embedded_sparse_tensor) |
输出结果为:
<tf.Variable 'Variable:0' shape=(2, 4) dtype=int64, numpy= array([[0, 1, 2, 3], [4, 5, 6, 7]])> <tf.Variable 'Variable:0' shape=(2, 4) dtype=int64, numpy= array([[ 8, 9, 10, 11], [12, 13, 14, 15]])> <tf.Variable 'Variable:0' shape=(2, 4) dtype=int64, numpy= array([[16, 17, 18, 19], [20, 21, 22, 23]])> ########## embedded_tensor ######### tf.Tensor( [[ 8 9 10 11] [16 17 18 19] [12 13 14 15] [ 4 5 6 7]], shape=(4, 4), dtype=int64) ########## embedded_sparse_tensor ######### tf.Tensor( [[20 22 24 26] [24 26 28 30] [24 26 28 30]], shape=(3, 4), dtype=int64) |
对第一个API embedding_ops.embedding_lookup,embedding矩阵由3个矩阵顺序排列,形成6*4的矩阵,4个样本的选择分别为1,2,4,3:
embedding矩阵为:
[ 0, 1, 2, 3] [ 4, 5, 6, 7] [ 8, 9, 10, 11] [12, 13, 14, 15] [16, 17, 18, 19] [20, 21, 22, 23] |
因为API调用中,用mod进行分区,取余的结果指向分区号,整除的结果执行分区里面的索引值。所以分区后表示如下,其中分区数为3个向量的数目,即3:
分区0,接受的id为id % 3 = 0,即id为0或3:
[ 0, 1, 2, 3] id = 0 (0/3 = 0) [ 4, 5, 6, 7] id = 3 (1/3 = 0) |
分区1,接受的id为id % 3 = 1,即id为1或4:
[ 8, 9, 10, 11] id = 1 (1/3 = 0) [12, 13, 14, 15] id = 4 (4/3 = 1) |
分区2,接受的id为id % 3 = 2,即id为2或5:
[16, 17, 18, 19] id = 2 (2/3 = 0) [20, 21, 22, 23] id = 5 (5/3 = 1) |
用4个样本进行选择后为:
[ 8 9 10 11] 1 [16 17 18 19] 2 [12 13 14 15] 4 [ 4 5 6 7] 3 |
API embedding_ops.embedding_lookup_sparse则用来对ids为一个稀疏矩阵的情况进行Embedding:
其中稀疏矩阵由SparseTensor生成,indices表示矩阵中的坐标,values表示对应坐标的值,即可以表示为单词样本中该位置的词在词库中的index值。
稀疏矩阵构成后如下:
[ 1 0 4 0] [ 0 2 1 0] [ 3 0 0 5] |
sparse_tensor = tf.SparseTensor(indices=[[0,0],[0,2],[1,1],[1,2],[2,0],[2,3]], values=[1,4,2,1,3,5],
dense_shape=[3,4])
如第一个样本,按照上面的逻辑,分别选择embedding矩阵中1和4
分区1,接受的id为id % 3 = 1
[ 8, 9, 10, 11] id = 1 (1/3 = 0) [12, 13, 14, 15] id = 4 (4/3 = 1) |
根据combiner=”sum”,结果为[20 22 24 26]
依次,整个稀疏矩阵embedding后的结果为:
[20 22 24 26] [24 26 28 30] [24 26 28 30] |
本作品采用知识共享署名 4.0 国际许可协议进行许可。