原创文章，转载请注明： 转载自慢慢的回味
Apollo的的规划算法基于Frenet坐标系，因此道路中心线的平滑性控制着车辆是否左右频繁晃动，而高精地图的道路中心线往往不够规划。Apollo在/modules/planning/reference_line中包含了多种参考线平滑算法：DiscretePointsReferenceLineSmoother（离散点平滑法，包括FEM_POS_DEVIATION_SMOOTHING有限元位置差异和COS_THETA_SMOOTHING余弦），QpSplineReferenceLineSmoother（三次样条插值法），SpiralReferenceLineSmoother（螺旋曲线法）。本篇以单元测试discrete_points_reference_line_smoother_test.cc的测试TEST_F(DiscretePointsReferenceLineSmootherTest, smooth)为例来分析Apollo对参考线reference line进行离散点平滑（FEM_POS_DEVIATION_SMOOTHING）的原理。
离散点平滑法原理
Apollo默认采用的平滑算法，其将参考线平滑构造成了一个二次优化问题，并使用osqp求解器进行求解。那么通过构建它的代价函数及约束条件就可以利用二次优化框架直接求解。
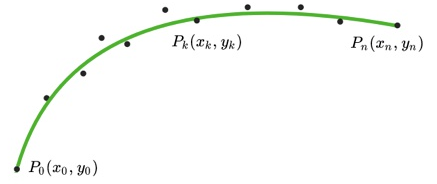
1 首先在参考线上隔相同距离打点（
），绿色的曲线就是算法将要得到的理想曲线。
2 然后列出代价函数：
![\[ cost=cost_{smooth}+cost_{length}+cost_{deviation} \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-b0f9ff0601118a0f4dd4ec25d6c1ca0a_l3.png "Rendered by QuickLaTeX.com")
其中，
为平滑度代价，
为长度代价，
为相对原始点偏离代价。
![\[ cost_{smooth}=\sum_{k=0}^{n-3}\parallel (x_k+x_{k+2})-2x_{k+1} \parallel^2_2 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-f64b22c128dd928b1369191984776b2f_l3.png "Rendered by QuickLaTeX.com")
![\[ cost_{length}=\sum_{k=0}^{n-2}\parallel y_{k+1}-y_k \parallel^2_2 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-8a4d80eb5930b977bb9c265eddbd6988_l3.png "Rendered by QuickLaTeX.com")
![\[ cost_{deviation}=\sum_{k=0}^{n-1}\parallel z_k-z_{k-ref} \parallel^2_2 \]](https://liuxiaofei.com.cn/blog/wp-content/ql-cache/quicklatex.com-e5f862bb92e076646dca64ebeb3f6a8d_l3.png "Rendered by QuickLaTeX.com")
要求相邻的3点尽量在同一条直线上，要求相邻2点不能太长，要求曲线上的点不能离参考点太远。在FEM_POS_DEVIATION_SMOOTHING算法中，的权重远远大于其它2个。
继续阅读“Apollo参考线优化之DiscretePointsReferenceLineSmoother”本作品采用知识共享署名 4.0 国际许可协议进行许可。